如图,在直三棱柱 $ABC-A_{1}B_{1}C_{1}$ 中,$\angle BAC=90^{\circ}$,$AB=a$,$AC=2$,$AA_{1}=1$.点 $D$ 在棱 $B_{1}C_{1}$ 上,且 $B_{1}D:DC_{1}=1:3$.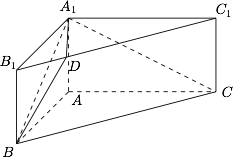

【难度】
【出处】
2013年全国高中数学联赛河北省预赛
【标注】
-
证明:$BD\perp A_{1}C$;标注答案略解析以 $A$ 为坐标原点,分别以 $AB$,$AC$,$AA_{1}$ 所在直线为 $x$ 轴,$y$ 轴,$z$ 轴建立空间直角坐标系,则\[D\left(\dfrac{3}{4}a,\dfrac{1}{2},1\right),\overrightarrow{BD}=\left(-\dfrac{a}{4},\dfrac{1}{2},1\right),\overrightarrow{A_{1}C}=(0,2,-1).\]因为$$\overrightarrow{BD}\cdot \overrightarrow{A_{1}C}=\left(-\dfrac{a}{4},\dfrac{1}{2},1\right)\cdot (0,2,-1)=0,$$所以 $\overrightarrow{BD}\perp \overrightarrow{A_{1}C}$,即 $BD\perp A_{1}C$.
-
当 $a$ 为何值时,二面角 $B-A_{1}D-B_{1}$ 的大小为 $60^{\circ}$?标注答案$\dfrac{2\sqrt 3}{3}$解析$\overrightarrow{A_{1}D}=\left(\dfrac{3}{4}a,\dfrac{1}{2},0\right)$,$\overrightarrow{A_{1}B}=(a,0,-1)$.
设 $\overrightarrow{n}=(x,y,1)$ 为平面 $A_{1}BD$ 的一个法向量,则$$\overrightarrow{n}\perp \overrightarrow{A_{1}D},\overrightarrow{n}\perp \overrightarrow{A_{1}B},$$即\[\begin{cases}(x,y,1)\cdot \left(\dfrac{3}{4}a,\dfrac{1}{2},0\right)=0,\\ (x,y,1)\cdot (a,0,-1)=0,\end{cases}\]化简得$$\begin{cases}\dfrac{3}{4}ax+\dfrac{y}{2}=0,\\ ax-1=0,\end{cases}$$解得 $\begin{cases}x=\dfrac{1}{a},\\ y=-\dfrac{3}{2},\end{cases}$ 故 $\overrightarrow{n}=\left(\dfrac{1}{a},-\dfrac{3}{2},1\right)$.
又 $\overrightarrow{m}=(0,0,1)$ 是平面 $A_{1}B_{1}C_{1}$ 的一个法向量,\[\begin{split}\cos\left\langle \overrightarrow{m},\overrightarrow{n}\right\rangle&=\dfrac{\overrightarrow m\cdot \overrightarrow n}{\left|\overrightarrow m\right|\cdot \left|\overrightarrow n\right|}\\&= \dfrac{(0,0,1)\cdot \left(\dfrac{1}{a},-\dfrac{3}{2},1\right)}{\sqrt{\left(\dfrac{1}{a}\right)^{2}+\left(-\dfrac{3}{2}\right)^{2}+1}}\\&=\dfrac{1}{\sqrt{\dfrac{1}{a^{2}}+\dfrac{13}{4}}}=\cos 60^{\circ}=\dfrac{1}{2}.\end{split}\]所以 $a=\dfrac{2}{\sqrt 3}$.
因此当 $a=\dfrac{2\sqrt 3}{3}$ 时,二面角 $B-A_{1}D-B_{1}$ 为 $60^{\circ}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2