设 $A,B,C$ 是椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 上的三个点，判断四边形 $OABC$ 能否为矩形．
【难度】
【出处】
无
【标注】
【答案】
当椭圆的离心率不小于 $\dfrac{\sqrt 6}3$ 时，四边形 $OABC$ 可能为矩形
【解析】
如图，连接 $AC,OB$ 且 $AC$ 与 $OB$ 相交于 $M$．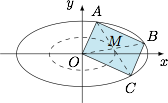
由于 $M$ 平分 $OB$，于是 $M$ 的轨迹是以原点为中心，对椭圆 $E$ 按 $2:1$ 的比例缩小得到的椭圆，记为 $E'$．又由于 $M$ 平分 $AC$，于是直线 $AC$ 与椭圆 $E'$ 相切于 $M$．接下来考虑 $\dfrac{AC}{OM}$，由于当 $M$ 从 $x$ 轴正半轴向 $y$ 轴正半轴运动时，$OM$ 单调递减，$AC$ 单调递增，因此 $\dfrac{AC}{2\cdot OM}$ 的取值范围是 $\left[\dfrac{\sqrt 3 b}{a},\dfrac{\sqrt 3 a}{b}\right]$．因此当 $a\geqslant \sqrt 3b$ 时，存在符合题意的矩形．
由于 $M$ 平分 $OB$，于是 $M$ 的轨迹是以原点为中心，对椭圆 $E$ 按 $2:1$ 的比例缩小得到的椭圆，记为 $E'$．又由于 $M$ 平分 $AC$，于是直线 $AC$ 与椭圆 $E'$ 相切于 $M$．接下来考虑 $\dfrac{AC}{OM}$，由于当 $M$ 从 $x$ 轴正半轴向 $y$ 轴正半轴运动时，$OM$ 单调递减，$AC$ 单调递增，因此 $\dfrac{AC}{2\cdot OM}$ 的取值范围是 $\left[\dfrac{\sqrt 3 b}{a},\dfrac{\sqrt 3 a}{b}\right]$．因此当 $a\geqslant \sqrt 3b$ 时，存在符合题意的矩形．
答案
解析
备注
