在椭圆中定义:过焦点且垂直于长轴的直线被椭圆截得的弦,叫做椭圆的通径.如图,已知椭圆 $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)$ 的左、右焦点分别为 $F_{1}$、$F_{2}$,其离心率为 $\dfrac{1}{2}$,通径长为 $3$.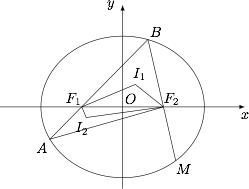

【难度】
【出处】
2013年全国高中数学联赛河北省预赛
【标注】
-
求椭圆的方程;标注答案$\dfrac{x^{2}}{4}+\dfrac{y^{2}}{3}=1$解析因为通径长为 $3$,由 $x=c$ 代入椭圆方程得$$y^{2}=\dfrac{b^{4}}{a^{2}}.$$由题意得$$\begin{cases}\dfrac{c}{a}=\dfrac{1}{2},\\\dfrac{2b^{2}}{a}=3,\\a^2+b^2=1,\end{cases} $$解得 $a=2$,$b=\sqrt 3$.
因此椭圆的方程为 $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{3}=1$. -
过 $F_{1}$ 的直线交椭圆于 $A,B$ 两点,$I_{1},I_{2}$ 分别为 $\triangle F_{1}BF_{2}$,$\triangle F_{1}AF_{2}$ 的内心,延长 $BF_{2}$ 交椭圆于点 $M$.
(i)求四边形 $F_{1}I_{2}F_{2}I_{1}$ 与 $\triangle AF_{2}B$ 的面积的比值 $p$;
(ii)在 $x$ 轴上是否存在定点 $C$,使 $\overrightarrow{CM}\cdot \overrightarrow{CB}$ 为常数?若存在,求出点 $C$ 的坐标;若不存在,说明理由.标注答案(i)$p=1:3$;(ii)存在,$C:\left(\dfrac{11}{8},0\right)$解析(i)设 $\triangle F_{1}BF_{2}$ 的内切圆的半径为 $r$.
因为椭圆的方程为 $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{3}=1$,$c=1$,所以\[\begin{split}&S_{\triangle F_{1}BF_{2}}=\dfrac{1}{2}\left(|BF_{1}|+|BF_{2}|+|F_{1}F_{2}|\right)\cdot r=3r,\\&S_{\triangle F_{1}I_{1}F_{2}} =\dfrac{1}{2}\cdot |F_{1}F_{2}|\cdot r=r.\end{split}\]则$$S_{\triangle F_{1}I_{1}F_{2}}:S_{\triangle F_{1}BF_{2}}=1:3,$$同理得,$$S_{\triangle F_{1}I_{2}F_{2}}:S_{\triangle F_{1}AF_{2}}=1:3.$$所以 $p=S_{ F_{1}I_{2}F_{2}I_{1}}:S_{\triangle AF_{2}B}=1:3$.
(ii)假设在 $x$ 轴上存在定点 $C(n,0)$,使 $\overrightarrow{CM}\cdot \overrightarrow{CB}$ 为常数.
设直线 $BM:x=my+1$,联立方程$$\begin{cases}x=my+1,\\ 3x^{2}+4y^{2}-12=0,\end{cases}$$得\[(3m^{2}+4)y^{2}+6my-9=0.\cdots\cdots\text{ ① }\]设 $B(x_{1},y_{1})$,$M(x_{2},y_{2})$,则$$\begin{split}y_{1}+y_{2}=-\dfrac{6m}{3m^{2}+4},\\y_{1}y_{2}=-\dfrac{9}{3m^{2}+4},\end{split}$$所以\[\begin{split}(x_{1}-n)(x_{2}-n)&=(my_{1}+1-n)(my_{2}+1-n)\\&=m^{2}y_{1}y_{2}+m(1-n)(y_{1}+y_{2})+(1-n)^{2}\\&=\dfrac{3m^{2}n^{2}-12m^{2}+4n^{2}-8n+4}{3m^{2}+4},\end{split}\]\[\begin{split}\overrightarrow{CM}\cdot \overrightarrow{CB}&=(x_{1}-n)(x_{2}-n)+y_{1}y_{2}\\&=\dfrac{3m^{2}n^{2}-12m^{2}+4n^{2}-8n-5}{3m^{2}+4}\\&=n^{2}-4-\dfrac{8n-11}{3m^{2}+4}.\end{split}\]因为 $\overrightarrow{CM}\cdot \overrightarrow{CB}$ 与 $m$ 无关,则 $n=\dfrac{11}{8}$ 时,\[\overrightarrow{CM}\cdot \overrightarrow{CB}=\left(\dfrac{11}{8}\right)^{2}-4=-\dfrac{135}{64}.\]故在 $x$ 轴上存在定点 $C\left(\dfrac{11}{8},0\right)$,使 $\overrightarrow{CM}\cdot \overrightarrow{CB}$ 为常数.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2