已知 $f(x)=ax^2+bx+c$（$a>0$），求证：最多存在两个整数 $s,t$，使得 $|f(s)|,|f(t)|$ 小于 $\dfrac a2$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
若 $f(x)\geqslant -\dfrac a2$ 恒成立，考虑 $f(x)=\dfrac a2$ 的根 $x_1,x_2$ 之间的距离：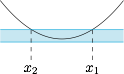
此时有$$\dfrac {4ac-b^2}{4a}\geqslant -\dfrac a2,$$即 $b^2-4ac\leqslant 2a^2$，于是$$|x_1-x_2|=\dfrac {\sqrt{b^2-4a\left(c-\dfrac a2\right)}}{a}=\dfrac {\sqrt{b^2-4ac+2a^2}}{a}\leqslant 2, $$故满足 $-\dfrac{a}{2}\leqslant f(x)\leqslant \dfrac{a}{2}$ 的整数最多只有两个；
若 $f(x)=-\dfrac a2$ 有两个不同的根 $x_3,x_4$，如图：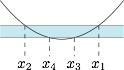
此时$$\dfrac {4ac-b^2}{4a}< -\dfrac a2,$$即 $b^2-4ac>2a^2$．考虑\[\begin{split} |x_1-x_2|-|x_3-x_4|=&\dfrac {\sqrt{b^2-4a\left(c-\dfrac a2\right)}}{a}-\dfrac {\sqrt{b^2-4a\left(c+\dfrac a2\right)}}{a}\\=&\dfrac{4a}{\sqrt{b^2-4ac+2a^2}+\sqrt{b^2-4ac-2a^2}}\\<&2.\end{split}\]即 $|x_4-x_2|+|x_1-x_3|<2$，从而区间 $[x_2,x_4]$ 与 $[x_3,x_1]$ 中最多各有一个整数，命题得证．
此时有$$\dfrac {4ac-b^2}{4a}\geqslant -\dfrac a2,$$即 $b^2-4ac\leqslant 2a^2$，于是$$|x_1-x_2|=\dfrac {\sqrt{b^2-4a\left(c-\dfrac a2\right)}}{a}=\dfrac {\sqrt{b^2-4ac+2a^2}}{a}\leqslant 2, $$故满足 $-\dfrac{a}{2}\leqslant f(x)\leqslant \dfrac{a}{2}$ 的整数最多只有两个；若 $f(x)=-\dfrac a2$ 有两个不同的根 $x_3,x_4$，如图：
此时$$\dfrac {4ac-b^2}{4a}< -\dfrac a2,$$即 $b^2-4ac>2a^2$．考虑\[\begin{split} |x_1-x_2|-|x_3-x_4|=&\dfrac {\sqrt{b^2-4a\left(c-\dfrac a2\right)}}{a}-\dfrac {\sqrt{b^2-4a\left(c+\dfrac a2\right)}}{a}\\=&\dfrac{4a}{\sqrt{b^2-4ac+2a^2}+\sqrt{b^2-4ac-2a^2}}\\<&2.\end{split}\]即 $|x_4-x_2|+|x_1-x_3|<2$，从而区间 $[x_2,x_4]$ 与 $[x_3,x_1]$ 中最多各有一个整数，命题得证．
答案
解析
备注
