设 $\left\{ {{x_n}} \right\}$ 为递增数列,${x_1} = 1$,${x_2} = 4$,在曲线 $y = \sqrt x $ 上与之对应的点列为 ${P_1}\left( {1,1} \right)$,${P_2}\left( {4,2} \right)$,${P_3}\left( {{x_3},\sqrt {{x_3}} } \right)$,…,${P_n}\left( {{x_n},\sqrt {{x_n}} } \right)$,…,且以 $O$ 为原点,由 $O{P_n}$、$O{P_{n + 1}}$ 与曲线 $O{P_{n + 1}}$ 所围成部分的面积为 ${S_n}$,若 $\left\{ {{S_n}} \right\}$($n \in {\mathbb{N}}$)是公比为 $\dfrac{4}{5}$ 的等比数列,试求 ${S_1} + {S_2} + \cdots + {S_n} + \cdots $ 和 $\mathop {\lim }\limits_{n \to \infty } {x_n}$.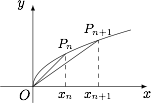

【难度】
【出处】
2001年上海交通大学连读班测试
【标注】
【答案】
$\dfrac {35}6$,$6\root 3 \of 6 $
【解析】
因为 ${P_1}\left( {1,1} \right)$,${P_2}\left( {4,2} \right)$,所以\[\begin{split}{S_1} &= \int_0^4 {\left( {\sqrt x - \dfrac{1}{2}x} \right){\mathrm d}x - \int_0^1 {\left( {\sqrt x - x} \right){\mathrm d}x} } \\&= \int_1^4 {\sqrt x {\mathrm d}x} - \int_0^4 {\dfrac{1}{2}x{\mathrm d}x} + \int_0^1 {x{\mathrm d}x}
\\&= \left. {\dfrac{2}{3}{x^{\frac{3}{2}}}} \right|_1^4 - \left. {\dfrac{1}{4}{x^2}} \right|_0^4 + \left. {\dfrac{1}{2}{x^2}} \right|_0^1 \\&= \dfrac{{14}}{3} - 4 + \dfrac{1}{2} = \dfrac{7}{6}.\end{split}\]因此$${S_n} = \dfrac{7}{6}{\left( {\dfrac{4}{5}} \right)^{n - 1}}.$$所以$${S_1} + {S_2} + \cdots + {S_n} + \cdots = \dfrac{{\dfrac{7}{6}}}{{1 - \dfrac{4}{5}}} = \dfrac{{35}}{6}.$$由于线段 $O{P_1}$ 与曲线 $O{P_1}$ 围成的面积为 $\dfrac{1}{6}$,所以设$$\mathop {\lim }\limits_{n \to \infty } {x_n} = m, P\left( {m,\sqrt m } \right).$$则曲线 $OP$ 与线段 $OP$ 围成的面积为 $\dfrac{1}{6} + \dfrac{{35}}{6} = 6$.
即\[\int_0^m {\left( {\sqrt x - \dfrac{1}{{\sqrt m }}x} \right){\mathrm d}x} = \left. {\dfrac{2}{3}{x^{\frac{3}{2}}} - \dfrac{1}{{2\sqrt m }}{x^2}} \right|_0^m = \dfrac{1}{6}{m^{\frac{3}{2}}} = 6,\]解得 $m = 6\root 3 \of 6 $.
\\&= \left. {\dfrac{2}{3}{x^{\frac{3}{2}}}} \right|_1^4 - \left. {\dfrac{1}{4}{x^2}} \right|_0^4 + \left. {\dfrac{1}{2}{x^2}} \right|_0^1 \\&= \dfrac{{14}}{3} - 4 + \dfrac{1}{2} = \dfrac{7}{6}.\end{split}\]因此$${S_n} = \dfrac{7}{6}{\left( {\dfrac{4}{5}} \right)^{n - 1}}.$$所以$${S_1} + {S_2} + \cdots + {S_n} + \cdots = \dfrac{{\dfrac{7}{6}}}{{1 - \dfrac{4}{5}}} = \dfrac{{35}}{6}.$$由于线段 $O{P_1}$ 与曲线 $O{P_1}$ 围成的面积为 $\dfrac{1}{6}$,所以设$$\mathop {\lim }\limits_{n \to \infty } {x_n} = m, P\left( {m,\sqrt m } \right).$$则曲线 $OP$ 与线段 $OP$ 围成的面积为 $\dfrac{1}{6} + \dfrac{{35}}{6} = 6$.
即\[\int_0^m {\left( {\sqrt x - \dfrac{1}{{\sqrt m }}x} \right){\mathrm d}x} = \left. {\dfrac{2}{3}{x^{\frac{3}{2}}} - \dfrac{1}{{2\sqrt m }}{x^2}} \right|_0^m = \dfrac{1}{6}{m^{\frac{3}{2}}} = 6,\]解得 $m = 6\root 3 \of 6 $.
答案
解析
备注