已知不等式 $ax^2-|x+1|+3a\geqslant 0$ 的解集为 $\mathbb R$,求 $a$ 的取值范围.
【难度】
【出处】
无
【标注】
【答案】
$\left[\dfrac 12,+\infty \right)$
【解析】
显然 $a>0$,于是问题等价于$$\forall x\in\mathbb R,x^2+3\geqslant \dfrac 1a\cdot |x+1|,$$如图.计算可知极限情况时 $\dfrac 1a=2$,因此可得 $a$ 的取值范围是 $\left[\dfrac 12,+\infty \right)$.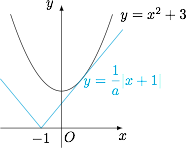
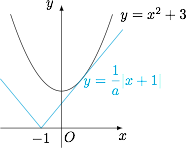
答案
解析
备注