$n(n\geqslant 5)$ 个球队进行足球比赛,任意两个队比赛一场,每天安排一场比赛.一个队相邻两场比赛之间的间隔天数称为该队这两场比赛的“间隔数”,例如某队前两场比赛安排在第一天和第三天,则间隔数为 $1$.
【难度】
【出处】
2011年全国高中数学联赛江苏省复赛加试
【标注】
-
对 $n=5$,设计一个赛程,使各队所有的间隔数均不小于 $1$;标注答案略解析设队号依次为 $1,2,3,4,5$.
设计一个满足题设的赛程如下: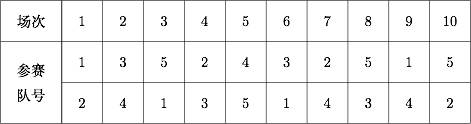
-
证明:间隔数的最小值不超过 $\left[\dfrac{n-3}{2}\right]$.标注答案略解析由条件知,要安排 $\dfrac{n(n-1)}{2}$ 场比赛.
情形一 $n$ 为奇数.
若某队所有的间隔数至少为$$\left[\dfrac{n-3}{2}\right]+1=\dfrac{n-1}{2},$$则从该队的第一场到第 $n-1$ 场比赛需要的天数至少为$$\left(\dfrac{n-1}{2}+1\right)(n-2)+1=\dfrac{n(n-1)}{2}.$$故最多只能有一个队的间隔数均大于 $\left[\dfrac{n-3}{2}\right]$.
结论成立.情形二 $n$ 为偶数.
此时至少有两个队(设为 $A$ 和 $B$)在前 $\dfrac n2 -1$ 天不参赛.
若它们所有的间隔数至少为$$\left[\dfrac{n-3}{2}\right]+1=\dfrac n2-1,$$则赛程的总天数至少为$$\dfrac n2 -1+\left(\dfrac n2-1+1\right)(n-2)+1=\dfrac{n(n-1)}{2}.$$故 $A$ 和 $B$ 只能同时参赛,矛盾.
所以至少有一个间隔数不超过 $\left[\dfrac{n-3}{2}\right]$,从而间隔数的最小值不超过 $\left[\dfrac{n-3}{2}\right]$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2