已知椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 的左、右焦点分别为 $F_1,F_2$.$P$ 是椭圆上一点,直线 $F_2M$ 垂直于 $OP$ 且交线段 $F_1P$ 于点 $M$,若 $F_1M=2MP$,求椭圆 $E$ 的离心率 $e$ 的取值范围.

【难度】
【出处】
无
【标注】
【答案】
$\left[\dfrac 12,1\right)$
【解析】
延长 $OF_2$ 至 $Q$,使得 $F_2Q=F_2O$,连接 $PQ$,则有 $MF_2\parallel PQ$,于是 $\angle OPQ$ 为直角,从而 $PF_2=c$,其中 $c$ 为椭圆 $E$ 的半焦距.因此$$a-c\leqslant c\leqslant a+c,$$解得 $e\geqslant \dfrac 12$,进而 $e$ 的取值范围是 $\left[\dfrac 12,1\right)$.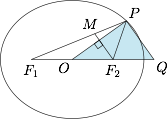

答案
解析
备注