设 $F_1,F_2$ 是椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的焦点,椭圆的弦 $AB$ 过焦点 $F_1$,求 $\triangle ABF_2$ 面积的最大值.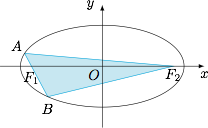

【难度】
【出处】
无
【标注】
【答案】
当 $a\geqslant \sqrt 2b$ 时,所求面积的最大值为 $ab$;当 $a<\sqrt 2b$ 时,所求面积的最大值为 $\dfrac{2b^2\sqrt{a^2-b^2}}a$
【解析】
设 $AF_1=m$,$BF_1=n$,则由椭圆的性质可得$$\dfrac 1m+\dfrac 1n=\dfrac{2a}{b^2},$$于是$$mn=\dfrac{b^2}{2a}\cdot AB.$$根据海伦公式,有\[\begin{split} S_{\triangle ABF_2}&=\sqrt{2a\cdot (2a-AB)\cdot (2a-BF_2)\cdot (2a-AF_2)}\\ &=\sqrt{2a(2a-AB)\cdot mn} \\ &=b\cdot \sqrt{(2a-AB)\cdot AB},\end{split}\]当椭圆的通径 $\dfrac {2b^2}a\leqslant a$,即 $a\geqslant \sqrt 2b$ 时,$S_{\triangle ABF_2}\leqslant ab$,当 $AB=a$ 时面积有最大值;
当 $a<\sqrt 2b$ 时,当 $AB=\dfrac {2b^2}a$ 时,面积取到最大值 $\dfrac{2b^2\sqrt{a^2-b^2}}a$.
当 $a<\sqrt 2b$ 时,当 $AB=\dfrac {2b^2}a$ 时,面积取到最大值 $\dfrac{2b^2\sqrt{a^2-b^2}}a$.
答案
解析
备注