设实数 $x,y$ 满足\[\begin{cases}
(x-1)\left(y^2+6\right)&=y\left(x^2+1\right),\\
(y-1)\left(x^2+6\right)&=x\left(y^2+1\right),
\end{cases}\]则 \((\qquad)\)
(x-1)\left(y^2+6\right)&=y\left(x^2+1\right),\\
(y-1)\left(x^2+6\right)&=x\left(y^2+1\right),
\end{cases}\]则 \((\qquad)\)
【难度】
【出处】
2017年清华大学THUSSAT测试题
【标注】
【答案】
BD
【解析】
题中方程组即\[\begin{cases} xy^2-x^2y-y^2+6x-y-6=0,\\
x^2y-xy^2-x^2+6y-x-6=0,\end{cases}\]也即\[\begin{cases} -x^2-y^5+5x+5y-12=0,\\
2xy^2-2x^y+x^2-y^2+7x-7y=0,\end{cases}\]整理得\[\begin{cases} \left(x-\dfrac 52\right)^2+\left(y-\dfrac 52\right)^2=\dfrac 12,\\ (x-y)(2xy-x-y-7)=0,\end{cases}\]如图,该方程组共有 $4$ 组解\[(x,y)=(2,2),(2,3),(3,2),(3,3).\]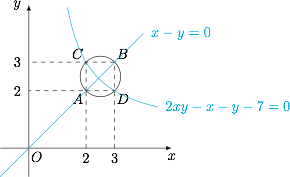
x^2y-xy^2-x^2+6y-x-6=0,\end{cases}\]也即\[\begin{cases} -x^2-y^5+5x+5y-12=0,\\
2xy^2-2x^y+x^2-y^2+7x-7y=0,\end{cases}\]整理得\[\begin{cases} \left(x-\dfrac 52\right)^2+\left(y-\dfrac 52\right)^2=\dfrac 12,\\ (x-y)(2xy-x-y-7)=0,\end{cases}\]如图,该方程组共有 $4$ 组解\[(x,y)=(2,2),(2,3),(3,2),(3,3).\]
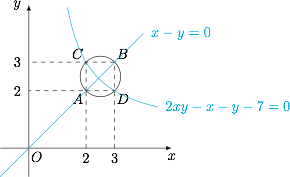
题目
答案
解析
备注