已知抛物线 $C_1:x^2=4y$ 的焦点 $F$ 也是椭圆 $C_2:\dfrac{y^2}{a^2}+\dfrac{x^2}{b^2}=1$($a>b>0$)的一个焦点,$C_1$ 与 $C_2$ 的公共弦的长为 $2\sqrt 6$.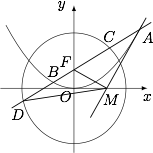

【难度】
【出处】
2015年高考湖南卷(理)
【标注】
-
求 $C_2$ 的方程;标注答案$\dfrac{x^2}{8}+\dfrac{y^2}{9}=1$解析根据题意,$F(0,1)$,而与抛物线 $C_1:x^2=4y$ 的公共弦的长为 $2\sqrt 6$,可以推得椭圆 $C_2$ 经过点 $\left(\sqrt 6,\dfrac 32\right)$,因此$$\begin{cases} a^2=b^2+1,\\\dfrac{9}{4a^2}+\dfrac{6}{b^2}=1,\end{cases}$$解得$$\begin{cases} a^2=9,\\b^2=8,\end{cases}$$所以椭圆的方程为 $\dfrac{x^2}{8}+\dfrac{y^2}{9}=1$.
-
过点 $F$ 的直线 $l$ 与 $C_1$ 相交于 $A,B$ 两点,与 $C_2$ 相交于 $C,D$ 两点,且 $\overrightarrow {AC}$ 与 $\overrightarrow {BD}$ 同向.
(i)若 $|AC|=|BD|$,求直线 $l$ 的斜率;
(ii)设 $C_1$ 在点 $A$ 处的切线与 $x$ 轴的交点为 $M$,证明:直线 $l$ 绕点 $F$ 旋转时,$\triangle MFD$ 总是钝角三角形.标注答案$k=\pm \dfrac{\sqrt 6}4$;略解析(i)根据题意 $|AB|=|CD|$,设直线 $l$ 的方程为 $l:y=kx+1$,$A,B,C,D$ 的横坐标分别为 $x_1,x_2,x_3,x_4$.
联立直线 $l$ 与抛物线 $C_1$ 的方程,可得$$x^2-4kx-4=0,$$于是$$|x_1-x_2|=\sqrt{16(k^2+1)};$$联立直线 $l$ 与椭圆 $C_2$ 的方程,可得$$\left(\dfrac 18+\dfrac 19k^2\right)x^2+\dfrac{2k}9x-\dfrac 89=0,$$于是$$|x_3-x_4|=\dfrac{\sqrt{\dfrac 49(k^2+1)}}{\dfrac 18+\dfrac 19k^2};$$而由 $|AB|=|CD|$ 可得$$\sqrt{1+k^2}\cdot |x_1-x_2|=\sqrt{1+k^2}\cdot |x_3-x_4|,$$因此$$\sqrt{16(k^2+1)}=\dfrac{\sqrt{\dfrac 49(k^2+1)}}{\dfrac 18+\dfrac 19k^2},$$解得 $k=\pm \dfrac{\sqrt 6}4$.
(ii)设 $A(4t,4t^2)$,则抛物线在点 $A$ 处的切线斜率为函数 $y=\dfrac 14x^2$ 在 $x=4t$ 处的导函数值,因此切线方程为$$y=2t(x-4t)+4t^2,$$因此可得点 $M$ 的坐标为 $M(2t,0)$.
于是$$\overrightarrow {FA}\cdot\overrightarrow {FM}=(4t,4t^2-1)\cdot (2t,-1)=4t^2+1>0,$$又 $A,F,M$ 三点不共线,因此 $\angle AFM$ 为锐角,进而 $\angle MFD$ 为钝角,因此 $\triangle MFD$ 恒为钝角三角形.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2