已知点 $F$ 是椭圆 $\dfrac{x^2}{25}+\dfrac{y^2}9=1$ 的左焦点,直线 $AB$ 经过 $F$ 且与椭圆交于 $A,B$ 两点.若 $O$ 为坐标原点,$\triangle AOB$ 的面积是 $\dfrac 92$,求直线 $AB$ 的斜率 $k$.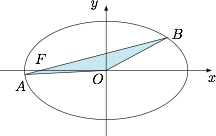

【难度】
【出处】
无
【标注】
【答案】
$\pm\dfrac{\sqrt{15}}{15}$
【解析】
设 $\angle BFO=\theta$,则$$S_{\triangle AOB}=\dfrac 12 \cdot 4\cdot \left(\dfrac{9}{5-4\cos\theta}+\dfrac{9}{5+4\cos\theta}\right)\cdot \sin\theta =\dfrac 92,$$整理得$$40\sin\theta =25-16\cos^2\theta,$$即$$(4\sin\theta -1)(4\sin\theta-9)=0,$$因此 $\sin\theta=\dfrac 14$,从而直线 $AB$ 的斜率 $k=\pm\dfrac{\sqrt{15}}{15}$.
答案
解析
备注