如图,$\triangle ABC$ 的内切圆切 $BC$ 边于 $D$,点 $E$,$F$ 分别是 $\triangle ABD$,$\triangle ACD$ 的内心,证明:$EF \perp AD$.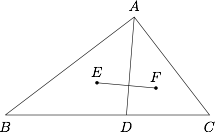

【难度】
【出处】
2014年全国高中数学联赛山西省预赛
【标注】
【答案】
略
【解析】
设 $\triangle ABD$,$\triangle ACD$ 的内切圆 $\odot E$,$\odot F$ 分别切 $BD$,$CD$ 于 $M$,$N$,而 $\triangle ABC$ 的内切圆与边 $AB$,$AC$ 分别切于点 $P$,$Q$,则$$AP=AQ,BD=BP,CD=CQ.$$因为$$DM=\dfrac {DA+DB-AB}{2}+\dfrac {DA+BP-AB}{2}=\dfrac {DA-AP}{2},$$及$$DN=\dfrac {DA+DC-AC}{2}+\dfrac {DA+CQ-AC}{2}=\dfrac {DA-AQ}{2},$$所以 $DM=DN$.
设 $ET_1 \perp AD$ 于 $T_1$,$FT_2 \perp AD$ 于 $T_2$,则$$\triangle DT_1E \cong \triangle DME, \triangle DT_2F \cong \triangle DNF.$$所以$$DT_1=DM=DN=DT_2,$$于是 $T_1$,$T_2$ 共点,记此点为 $T$,而由$$ \angle DTE =\angle DME=90^{\circ}=\angle DNF =DTF,$$得$$\angle DTE +\angle DTF=180^{\circ}.$$即有 $E$,$T$,$F$ 共线.
因此,$EF \perp AD$(也即 $\odot E$,$\odot F$ 切于 $AD$ 上的同一点 $T$).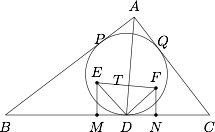
设 $ET_1 \perp AD$ 于 $T_1$,$FT_2 \perp AD$ 于 $T_2$,则$$\triangle DT_1E \cong \triangle DME, \triangle DT_2F \cong \triangle DNF.$$所以$$DT_1=DM=DN=DT_2,$$于是 $T_1$,$T_2$ 共点,记此点为 $T$,而由$$ \angle DTE =\angle DME=90^{\circ}=\angle DNF =DTF,$$得$$\angle DTE +\angle DTF=180^{\circ}.$$即有 $E$,$T$,$F$ 共线.
因此,$EF \perp AD$(也即 $\odot E$,$\odot F$ 切于 $AD$ 上的同一点 $T$).

答案
解析
备注