如图，$A$，$B$ 是椭圆 $\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1(a>b>0)$ 的长轴端点，$P$ 是椭圆上异于 $A$，$B$ 的点，自 $A$，$B$ 分别作 $l_1\perp PA$，$l_2 \perp PB$，$l_1$，$l_2$ 相交于点 $M$．当动点 $P$ 在椭圆上移动时，求点 $M$ 的轨迹方程．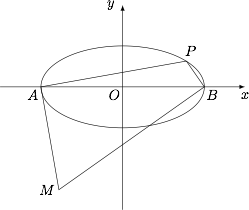
【难度】
【出处】
2014年全国高中数学联赛山西省预赛
【标注】
【答案】
$\dfrac {x^2}{a^2}+\dfrac {y^2}{\left(\dfrac {a^2}{b}\right)^2}=1$，$(|x|<a)$
【解析】
据条件知，$A$，$P$，$B$，$M$ 共圆，其圆心 $N$ 在弦 $AB$ 的中垂线 $y$ 轴上，其坐标设为 $N(0,t)$．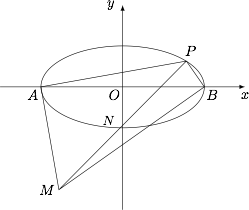
又设点 $P$，$M$ 的坐标为 $P(x_0,y_0)$，$M(x,y)$．
因为 $N$ 是直径 $PM$ 的中点，所以$$x_0=-x,y+y_0=2t,$$因此$$y_0=2t-y.$$点 $P$ 在椭圆上，则$$\dfrac {x_0^2}{a^2}+\dfrac {y_0^2}{b^2}=1,$$即有$$\dfrac {x ^2}{a^2}+\dfrac {(2t-y)^2}{b^2}=1.\quad\cdots\cdots \text{ ① }$$又由 $NA=NM$，得$$t^2+a^2=(t-y)^2+x^2,$$所以$$t=\dfrac {x^2+y^2-a^2}{2y},\quad\cdots\cdots \text{ ② }$$由 ①② 得，$$\dfrac {x ^2}{a^2}+\left(\dfrac {x^2-a^2}{by}\right)^2=1,$$即$$\dfrac {x ^2-a^2}{a^2}+\left(\dfrac {x^2-a^2}{by}\right)^2=0,\quad\cdots\cdots \text{ ③ }$$由于 $|x|<|x_0|<a$，故$$x^2-a^2 \neq 0,$$因此由 ③ 得，$$\dfrac {1}{a^2}+\dfrac {x^2-a^2}{b^2y^2}=0,$$即$$\dfrac {y^2}{a^2}+\dfrac {x^2}{b^2}=\dfrac {a^2}{b^2},$$也即$$\dfrac {x^2}{a^2}+\dfrac {y^2}{\left(\dfrac {a^2}{b}\right)^2}=1,(|x|<a),$$其轨迹为一个椭圆（去掉其与 $x$ 轴的两个交点 $(\pm a, 0)$）．
又设点 $P$，$M$ 的坐标为 $P(x_0,y_0)$，$M(x,y)$．因为 $N$ 是直径 $PM$ 的中点，所以$$x_0=-x,y+y_0=2t,$$因此$$y_0=2t-y.$$点 $P$ 在椭圆上，则$$\dfrac {x_0^2}{a^2}+\dfrac {y_0^2}{b^2}=1,$$即有$$\dfrac {x ^2}{a^2}+\dfrac {(2t-y)^2}{b^2}=1.\quad\cdots\cdots \text{ ① }$$又由 $NA=NM$，得$$t^2+a^2=(t-y)^2+x^2,$$所以$$t=\dfrac {x^2+y^2-a^2}{2y},\quad\cdots\cdots \text{ ② }$$由 ①② 得，$$\dfrac {x ^2}{a^2}+\left(\dfrac {x^2-a^2}{by}\right)^2=1,$$即$$\dfrac {x ^2-a^2}{a^2}+\left(\dfrac {x^2-a^2}{by}\right)^2=0,\quad\cdots\cdots \text{ ③ }$$由于 $|x|<|x_0|<a$，故$$x^2-a^2 \neq 0,$$因此由 ③ 得，$$\dfrac {1}{a^2}+\dfrac {x^2-a^2}{b^2y^2}=0,$$即$$\dfrac {y^2}{a^2}+\dfrac {x^2}{b^2}=\dfrac {a^2}{b^2},$$也即$$\dfrac {x^2}{a^2}+\dfrac {y^2}{\left(\dfrac {a^2}{b}\right)^2}=1,(|x|<a),$$其轨迹为一个椭圆（去掉其与 $x$ 轴的两个交点 $(\pm a, 0)$）．
答案
解析
备注
