如图,过 $\triangle ABC$ 的三个顶点 $A,B,C$ 各作其外接圆的切线,分别与相应顶点的对边所在的直线相交,证明:三个交点 $D,E,F$ 共线.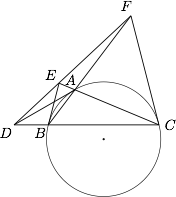

【难度】
【出处】
2013年全国高中数学联赛山西省预赛
【标注】
【答案】
略
【解析】
据梅涅劳斯定理逆定理,只要证\[\dfrac{BD}{DC}\cdot \dfrac{CE}{EA}\cdot \dfrac{AF}{FB}=1.\]由弦切角关系\[\angle BAD=\angle ACB=\angle ABE,\angle ABC=\angle ACF,\]由 $\triangle BAD\backsim \triangle ACD$,得\[\dfrac{BD}{DC}=\dfrac{S_{\triangle ABD}}{S_{\triangle ADC}}=\left(\dfrac{BA}{AC}\right)^{2},\]由 $\triangle CEB\backsim \triangle BEA$,得\[\dfrac{CE}{EA}=\dfrac{S_{\triangle BCE}}{S_{\triangle BEA}}=\left(\dfrac{BC}{AB}\right)^{2},\]由 $\triangle CFA\backsim \triangle BFC$,得\[\dfrac{AF}{FB}=\dfrac{S_{\triangle CAF}}{S_{\triangle CFB}}=\left(\dfrac{CA}{BC}\right)^{2},\]所以\[\dfrac{BD}{DC}\cdot \dfrac{CE}{EA}\cdot \dfrac{AF}{FB}=\dfrac{S_{\triangle ABD}}{S_{\triangle ADC}}\cdot \dfrac{S_{\triangle BCE}}{S_{\triangle BEA}}\cdot \dfrac{S_{\triangle CAF}}{S_{\triangle CFB}}=1,\]因此 $D,E,F$ 三点共线.
答案
解析
备注