如图，正方形 $ABCD$ 中，$E$ 为 $AB$ 的中点，$P$ 为以 $A$ 为圆心的弧 $BD$ 上一点（包含端点），且 $\overrightarrow{AC}=\lambda\overrightarrow{DE}+\mu\overrightarrow{AP}$，求 $\lambda+\mu$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$\left[\dfrac 12,5\right]$
【解析】
本题可以通过共线向量的系数和关系，直接结合图象得到范围，将正方形 $ABCD$ 往下平移，使得两个正方形恰有一条边重合，如图，记 $F$ 为 $E$ 平移后得到的点，则 $\overrightarrow {DE}=\overrightarrow {AF}$，于是$$\overrightarrow {AC}=\lambda \overrightarrow {AF}+\mu\overrightarrow {AP}.$$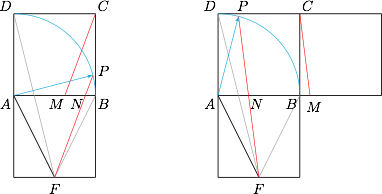
连结 $PF$，交 $AB$ 于点 $N$，过 $C$ 作 $PF$ 的平行线交 $AB$ 或其延长线于点 $M$，则有$$\lambda+\mu=\dfrac {AM}{AN}.$$当点 $P$ 与点 $B$ 移动到点 $D$ 时，$AN$ 从 $1$（正方形边长）减少到 $\dfrac 14$；同时 $AM$ 的长从 $\dfrac 12$ 增加到 $\dfrac 54$，从而得到 $\lambda +\mu\in\left[\dfrac 12,5\right ]$．
类似这样的思路可以不考虑与 $AB$ 的交点，考虑 $BF$ 与 $AC$ 及其延长线的交点，由交点的位置去得到 $\lambda +\mu$ 的值．
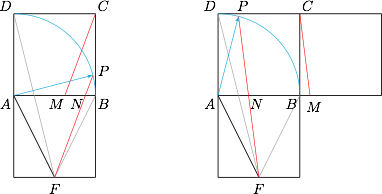连结 $PF$，交 $AB$ 于点 $N$，过 $C$ 作 $PF$ 的平行线交 $AB$ 或其延长线于点 $M$，则有$$\lambda+\mu=\dfrac {AM}{AN}.$$当点 $P$ 与点 $B$ 移动到点 $D$ 时，$AN$ 从 $1$（正方形边长）减少到 $\dfrac 14$；同时 $AM$ 的长从 $\dfrac 12$ 增加到 $\dfrac 54$，从而得到 $\lambda +\mu\in\left[\dfrac 12,5\right ]$．类似这样的思路可以不考虑与 $AB$ 的交点，考虑 $BF$ 与 $AC$ 及其延长线的交点，由交点的位置去得到 $\lambda +\mu$ 的值．
答案
解析
备注
