已知等腰三角形 $ABC$ 的底 $BC$ 长为 $6$，腰 $AB$ 长为 $5$．设 $D$ 是底边 $BC$ 上一点，以 $AD$ 为边向两边作等边三角形 $ADE,ADF$，设 $DE,DF$ 分别交 $AB,AC$ 于点 $M,N$，求证：当 $D$ 位于 $BC$ 中点时 $DM+DN$ 取得最小值．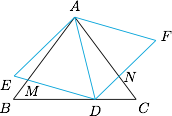
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
在 $DE$ 上取 $DG=FN$，则 $\triangle ADN$ 与 $\triangle AEG$ 全等，如图：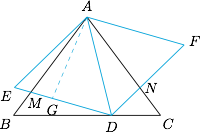
因此$$DM+DN=DM+GE=DE+GM=AD+GM,$$而当 $D$ 位于 $BC$ 中点时，$AD$ 和 $GM$ 同时取得最小值（注意 $G$ 点的轨迹是延长线通过点 $A$ 的线段）．
因此$$DM+DN=DM+GE=DE+GM=AD+GM,$$而当 $D$ 位于 $BC$ 中点时，$AD$ 和 $GM$ 同时取得最小值（注意 $G$ 点的轨迹是延长线通过点 $A$ 的线段）．
答案
解析
备注
