如图，椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的离心率是 $\dfrac{\sqrt 2}2$，过点 $P(0,1)$ 的动直线 $l$ 与椭圆相交于 $A,B$ 两点．当直线 $l$ 平行于 $x$ 轴时，直线 $l$ 被椭圆 $E$ 截得的线段长为 $2\sqrt 2$．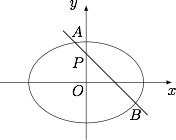
【难度】
【出处】
2015年高考四川卷（理）
【标注】
-
求椭圆 $E$ 的方程；标注答案$\dfrac{x^2}4+\dfrac{y^2}2=1$解析根据题意，椭圆过点 $(\sqrt 2,1)$ 且离心率为 $\dfrac{\sqrt 2}2$，因此 $E:\dfrac{x^2}4+\dfrac{y^2}2=1$．
-
在平面直角坐标系 $xOy$ 中，是否存在与点 $P$ 不同的定点 $Q$，使得 $\dfrac{|QA|}{|QB|}=\dfrac{|PA|}{|PB|}$ 恒成立？若存在，求出点 $Q$ 的坐标；若不存在，请说明理由．标注答案$Q$ 点存在，坐标为 $(0,2)$解析若 $Q$ 点存在，则 $Q$ 一定在 $y$ 轴上，不妨设 $Q(0,m)$．
当直线 $AB$ 的斜率不存在时，由 $\dfrac{|QA|}{|QB|}=\dfrac{|PA|}{|PB|}$ 可得 $Q(0,2)$．
当直线 $AB$ 的斜率存在时，根据题意，可知 $QP$ 是 $\angle AQB$ 的平分线，因此直线 $AQ$ 与直线 $BQ$ 的斜率之和为 $0$．
设直线 $AB$ 的方程为 $y=kx+1$，$A(x_1,y_1)$，$B(x_2,y_2)$，则直线 $AQ$ 与直线 $BQ$ 的斜率之和\[\begin{split} k_{AQ}+k_{BQ}&=\dfrac{y_1-m}{x_1}+\dfrac{y_2-m}{x_2}\\&=\dfrac{kx_1+1-m}{x_1}+\dfrac{kx_2+1-m}{x_2}\\&=2k+(1-m)\cdot\dfrac{x_1+x_2}{x_1x_2},\end{split}\]将直线 $AB$ 的方程与椭圆 $E$ 的方程联立可得$$(1+2k^2)x^2+4kx-2=0,$$因此利用韦达定理可以计算得$$k_{AQ}+k_{BQ}=2k+(1-m)\cdot 2k=2k(2-m),$$因此当 $m=2$ 时符合题意．
综上 $Q$ 点存在，且坐标为 $(0,2)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
