已知函数 $f(x)=\dfrac{2(1-a)+\cos x}{a-\sin^2x}$ 的值域包含区间 $[1,2]$,求 $a$ 的取值范围.
【难度】
【出处】
无
【标注】
【答案】
$\left[\dfrac 13,\dfrac 34\right)\cup\left(\dfrac 34,\dfrac {33}{32}\right]$
【解析】
函数 $y=\dfrac{x+2a}{x^2-a}$ 可以看成是抛物线 $x=y^2$($-1\leqslant y\leqslant 1$)的点与直线 $y=-2x$ 上的点连线的斜率,如图.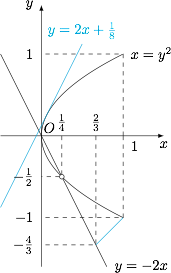

答案
解析
备注