已知椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的上顶点为 $B$,左焦点为 $F$,离心率为 $\dfrac{\sqrt 5}5$.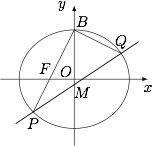

【难度】
【出处】
2015年高考天津卷(文)
【标注】
-
求直线 $BF$ 的斜率;标注答案$2$解析直线 $BF$ 的斜率为$$\dfrac bc=\sqrt{\dfrac{a^2-c^2}{c^2}}=\sqrt{\dfrac{1}{e^2}-1}=2.$$
-
设直线 $BF$ 与椭圆交于 $P$($P$ 异于点 $B$),过点 $B$ 且垂直于 $BP$ 的直线与椭圆交于点 $Q$($Q$ 异于点 $B$),直线 $PQ$ 与 $y$ 轴交于点 $M$,$|PM|=\lambda |MQ|$.
(i)求 $\lambda$ 的值;
(ii)若 $|PM|\sin\angle BQP=\dfrac{7\sqrt 5}9$,求椭圆的方程.标注答案(i)$\dfrac 78$.(ii)$\dfrac{x^2}{5}+\dfrac{y^2}4=1$解析由椭圆的离心率为 $\dfrac{\sqrt 5}5$,可得 $a^2=\dfrac 54b^2$,因此椭圆方程为 $\dfrac{4x^2}{5b^2}+\dfrac{y^2}{b^2}=1$.
设过点 $B$ 的直线 $y=kx+b$ 与椭圆交于另一点 $N$,则联立该直线方程与椭圆方程,得$$(4+5k^2)x^2+10kbx=0,$$于是 $N$ 点的横坐标为 $-\dfrac{10kb}{4+5k^2}$.
当 $k$ 取 $2$ 时,可得 $P$ 点的横坐标 $x_P=-\dfrac{5b}6$;
当 $k$ 取 $-\dfrac 12$ 时,可得 $Q$ 点的横坐标 $x_Q=\dfrac{20b}{21}$.
(i)根据题意,$\lambda=\left|\dfrac{x_P}{x_Q}\right|=\dfrac 78$.
(ii)根据题意,结合(i)中的结论有$$|PM|\sin\angle BQP=\dfrac 7{15}\cdot |PQ|\cdot\sin\angle BQP=\dfrac 7{15}\cdot |BP|=\dfrac{7\sqrt 5}9,$$于是 $|BP|=\dfrac{5\sqrt 5}3$;
另一方面,由弦长公式,有$$|BP|=\sqrt{1^2+2^2}\cdot\big|x_P-0\big|=\dfrac{5\sqrt 5 b}6,$$因此可得 $b=2$,从而椭圆方程为 $\dfrac{x^2}{5}+\dfrac{y^2}4=1$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2