设圆 $x^2+y^2+2x-15=0$ 的圆心为 $A$，直线 $l$ 过点 $B(1,0)$ 且与 $x$ 轴不重合，$l$ 交圆 $A$ 于 $C,D$ 两点，过 $B$ 作 $AC$ 的平行线交 $AD$ 于点 $E$．
【难度】
【出处】
2016年高考全国乙卷（理）
【标注】
-
证明：$|EA|+|EB|$ 为定值，并写出点 $E$ 的轨迹方程；标注答案$\dfrac{x^2}{4}+\dfrac{y^2}3=1(y\neq 0)$解析将圆的方程化为标准方程$$(x+1)^2+y^2=16.$$
由于 $BE\parallel AC$，于是 $\angle EBD=\angle ACD$．又 $|AC|=|AD|$，于是 $\angle ACD=\angle ADC$，因此 $\angle EBD=\angle EDB$，从而 $|EB|=|ED|$，这样就得到了$$|EA|+|EB|=|EA|+|ED|=|AD|$$为定值 $4$．根据椭圆的定义，点 $E$ 的轨迹方程为$$\dfrac{x^2}{4}+\dfrac{y^2}3=1(y\neq 0).$$ -
设点 $E$ 的轨迹为曲线 $C_1$，直线 $l$ 交 $C_1$ 于 $M,N$ 两点，过 $B$ 且与 $l$ 垂直的直线与圆 $A$ 交于 $P,Q$ 两点，求四边形 $MPNQ$ 面积的取值范围．标注答案$[12,8\sqrt 3)$解析设 $\angle MBA=\theta$（$\theta \in (0,\pi)$），则在 $\triangle MAB$ 中应用余弦定理，有$$|MA|^2=|MB|^2+|AB|^2-2\cdot |MB|\cdot |AB|\cdot\cos\theta,$$结合 $|MA|+|MB|=4$ 可解得$$|MB|=\dfrac{3}{2-\cos\theta}.$$
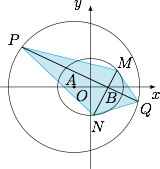类似的，可得$$|NB|=\dfrac{3}{2+\cos\theta},$$从而$$|MN|=|MB|+|NB|=\dfrac{12}{4-\cos^2\theta}.$$此时直线 $PQ$ 的方程为$$x\cos\theta =y\sin\theta +\cos\theta,$$于是圆的弦长$$|PQ|=2\sqrt{4^2-\left(\dfrac{2\cos\theta}{\sqrt{\cos^2\theta+\sin^2\theta}}\right)^2}=4\sqrt{4-\cos^2\theta}.$$于是可得四边形 $MPNQ$ 的面积$$S=\dfrac 12\cdot |MN|\cdot |PQ|=\dfrac{24}{\sqrt{4-\cos^2\theta}},$$于是四边形 $MPNQ$ 的面积的取值范围是 $[12,8\sqrt 3)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
