在锐角三角形 $ABC$ 中，$\angle A=\dfrac{\pi}{3}$，设在其内部同时满足 $PA\leqslant PB$ 和 $PA\leqslant PC$ 的点 $P$ 的全体形成的区域 $G$ 的面积为三角形 $ABC$ 面积的 $\dfrac 13$．证明：三角形 $ABC$ 为等边三角形．
【难度】
【出处】
2011年浙江省高中数学竞赛
【标注】
【答案】
略
【解析】
作 $\triangle{ABC}$ 的外接圆 $O$，作 $OE\perp AB$ 于 $E$，$OF\perp AC$ 于 $F$，$OM\perp BC$ 于 $M$，则区域 $G$ 为四边形 $AEOF$．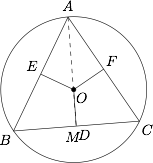
因为\[\begin{split}&S_{\text{四边形}AEOF}=\dfrac 13 S_{\triangle{ABC}},\\&2S_{\text{四边形}AEOF}=2S_{\triangle{AEO}}+2S_{\triangle{AOF}}=S_{\triangle{AOB}}+S_{\triangle{AOC}},\end{split}\]所以$$S_{\triangle{OBC}}=\dfrac 13 S_{\triangle{ABC}}.$$由已知 $\angle{BOC}=120^{\circ}$，则 $\angle{OBC}=30^{\circ}$，所以$$OM=\dfrac 12 R$$（$R$ 为 $\triangle{ABC}$ 的外接圆半径）．
作 $AD\perp BC$ 于 $D$，则\[\begin{split}&AD\geqslant AO+OM=\dfrac 32 R,\\&S_{\triangle{ABC}}\geqslant \dfrac 12 \times \dfrac{3R}{2}BC=3S_{\triangle{OBC}},\end{split}\]等号当且仅当 $A,O,M$ 共线，即 $\triangle{ABC}$ 为等边三角形．
因为\[\begin{split}&S_{\text{四边形}AEOF}=\dfrac 13 S_{\triangle{ABC}},\\&2S_{\text{四边形}AEOF}=2S_{\triangle{AEO}}+2S_{\triangle{AOF}}=S_{\triangle{AOB}}+S_{\triangle{AOC}},\end{split}\]所以$$S_{\triangle{OBC}}=\dfrac 13 S_{\triangle{ABC}}.$$由已知 $\angle{BOC}=120^{\circ}$，则 $\angle{OBC}=30^{\circ}$，所以$$OM=\dfrac 12 R$$（$R$ 为 $\triangle{ABC}$ 的外接圆半径）．作 $AD\perp BC$ 于 $D$，则\[\begin{split}&AD\geqslant AO+OM=\dfrac 32 R,\\&S_{\triangle{ABC}}\geqslant \dfrac 12 \times \dfrac{3R}{2}BC=3S_{\triangle{OBC}},\end{split}\]等号当且仅当 $A,O,M$ 共线，即 $\triangle{ABC}$ 为等边三角形．
答案
解析
备注
