设长方体的三边长为 $a,b,c$，且 $a > b > c$．设 $PQ$ 为此长方体的体对角线．求从 $P$ 沿长方体表面至 $Q$ 最短路径的长度．
【难度】
【出处】
2007年北京大学自主招生保送生测试
【标注】
【答案】
$\sqrt {{a^2} + {{\left( {b + c} \right)}^2}} $
【解析】
三种不同的方式，长度分别为 $\sqrt {{a^2} + {{\left( {b + c} \right)}^2}} $，$\sqrt {{b^2} + {{\left( {a + c} \right)}^2}} $，$\sqrt {{c^2} + {{\left( {a + b} 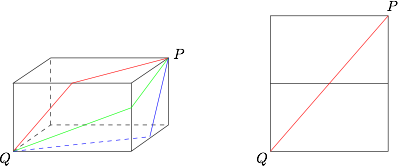\right)}^2}} $，
即$$\sqrt {{a^2} + {b^2} + {c^2} + 2bc} ,\sqrt {{a^2} + {b^2} + {c^2} + 2ca} ,\sqrt {{a^2} + {b^2} + {c^2} + 2ab} .$$因为 $a > b > c$，所以 $ab > ca > bc$，所以最短路径的长度为 $\sqrt {{a^2} + {{\left( {b + c} \right)}^2}} $．
即$$\sqrt {{a^2} + {b^2} + {c^2} + 2bc} ,\sqrt {{a^2} + {b^2} + {c^2} + 2ca} ,\sqrt {{a^2} + {b^2} + {c^2} + 2ab} .$$因为 $a > b > c$，所以 $ab > ca > bc$，所以最短路径的长度为 $\sqrt {{a^2} + {{\left( {b + c} \right)}^2}} $．
答案
解析
备注
