$AB$ 为过抛物线 ${y^2} = 4x$ 焦点 $F$ 的弦，$O$ 为坐标原点，且 $\angle OFA=135^\circ$，且 $E$ 为抛物线准线与 $x$ 轴的交点，则 $\angle AEB$ 的正切值为 \((\qquad)\)
【难度】
【出处】
2011年清华大学等七校联考自主招生试题
【标注】
【答案】
A
【解析】
如图，作 $AH\perp x$ 轴于点 $H$．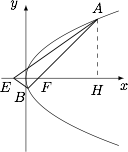
根据抛物线的性质，有 $\angle AEB=2\angle AEH$，而\[\tan\angle AEH=\dfrac{AH}{EH}=\dfrac{AH}{AF}=\dfrac{1}{\sqrt 2},\]于是\[\tan\angle AEB=2\sqrt 2.\]
根据抛物线的性质，有 $\angle AEB=2\angle AEH$，而\[\tan\angle AEH=\dfrac{AH}{EH}=\dfrac{AH}{AF}=\dfrac{1}{\sqrt 2},\]于是\[\tan\angle AEB=2\sqrt 2.\]
题目
答案
解析
备注
