$0 < \alpha < \dfrac{\pi }{2}$，求证：$\sin \alpha < \alpha < \tan \alpha $．
【难度】
【出处】
2010年北京大学等三校联考自主招生保送生测试
【标注】
【答案】
略
【解析】
利用三角函数线，如图．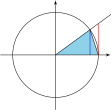
三个面积满足$$\frac{1}{2} \cdot 1 \cdot \sin \alpha < \frac{1}{2} \cdot \alpha \cdot 1 < \frac{1}{2} \cdot \tan \alpha \cdot 1$$所以 $\sin \alpha < \alpha < \tan \alpha $．
三个面积满足$$\frac{1}{2} \cdot 1 \cdot \sin \alpha < \frac{1}{2} \cdot \alpha \cdot 1 < \frac{1}{2} \cdot \tan \alpha \cdot 1$$所以 $\sin \alpha < \alpha < \tan \alpha $．
答案
解析
备注
