$P,Q$ 是边长为 $1$ 的正五边形边上的点．证明：线段 $PQ$ 最长为 $\dfrac{{\sqrt 5 + 1}}{2}$．
【难度】
【出处】
2010年北京大学等三校联考自主招生保送生测试
【标注】
【答案】
略
【解析】
如图左，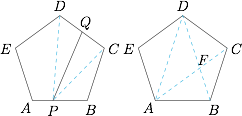
不妨设 $P \in AB$，若 $Q$ 在某条边上，以 $CD$ 为例，则 $\overrightarrow {PQ} = \lambda \overrightarrow {PC} + \left( {1 - \lambda } \right)\overrightarrow {PD} $，$$\left| {\overrightarrow {PQ} } \right| = \left| {\lambda \overrightarrow {PC} + \left( {1 - \lambda } \right)\overrightarrow {PD} } \right| \leqslant \lambda \left| {\overrightarrow {PC} } \right| + \left( {1 - \lambda } \right)\left| {\overrightarrow {PD} } \right|.$$于是用反证法容易证明$$\max \left( {PC{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} PD} \right) \geqslant PQ.$$也可以通过 $\angle PQD+\angle PQC=\pi$，得到 $\max\{\angle PQD,\angle PQC\}\geqslant \dfrac {\pi}2$，于是有 $\max\{PD,PC\}\geqslant PQ$．
因此当线段 $PQ$ 最长时，$Q$ 点在正五边形的顶点位置．
类似可证当线段 $PQ$ 最长时，$P$ 也在正五边形的顶点位置．
综上，正五边形的对角线长度为所求．
下面求正五边形的对角线长：
如上图右，$DF = AF = AB = 1$，设 $AD = x$ 为所求，则$$\dfrac{{AD}}{{AB}} = \frac{{AF}}{{BF}},$$即$$\dfrac{x}{1} = \dfrac{1}{{x - 1}},$$解得 $x = \dfrac{{1 + \sqrt 5 }}{2}$（负根舍去），因此原命题得证．
不妨设 $P \in AB$，若 $Q$ 在某条边上，以 $CD$ 为例，则 $\overrightarrow {PQ} = \lambda \overrightarrow {PC} + \left( {1 - \lambda } \right)\overrightarrow {PD} $，$$\left| {\overrightarrow {PQ} } \right| = \left| {\lambda \overrightarrow {PC} + \left( {1 - \lambda } \right)\overrightarrow {PD} } \right| \leqslant \lambda \left| {\overrightarrow {PC} } \right| + \left( {1 - \lambda } \right)\left| {\overrightarrow {PD} } \right|.$$于是用反证法容易证明$$\max \left( {PC{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} PD} \right) \geqslant PQ.$$也可以通过 $\angle PQD+\angle PQC=\pi$，得到 $\max\{\angle PQD,\angle PQC\}\geqslant \dfrac {\pi}2$，于是有 $\max\{PD,PC\}\geqslant PQ$．因此当线段 $PQ$ 最长时，$Q$ 点在正五边形的顶点位置．
类似可证当线段 $PQ$ 最长时，$P$ 也在正五边形的顶点位置．
综上，正五边形的对角线长度为所求．
下面求正五边形的对角线长：
如上图右，$DF = AF = AB = 1$，设 $AD = x$ 为所求，则$$\dfrac{{AD}}{{AB}} = \frac{{AF}}{{BF}},$$即$$\dfrac{x}{1} = \dfrac{1}{{x - 1}},$$解得 $x = \dfrac{{1 + \sqrt 5 }}{2}$（负根舍去），因此原命题得证．
答案
解析
备注
