如图所示，已知由 $\triangle{ABC}$ 的顶点 $A$ 引出的两条射线 $AX,AY$ 分别交 $BC$ 于点 $X,Y$，求证：$AB^2\cdot CY\cdot CX=AC^2\cdot BX\cdot BY$ 成立的充要条件是 $\angle{BAX}=\angle{CAY}$．
【难度】
【出处】
2011年湖南省高中数学竞赛
【标注】
【答案】
略
【解析】
充分性：
若 $\angle{BAX}=\angle{CAY}$，设 $\angle{BAX}=\angle{CAY}=\alpha$，$\angle{XAY}=\theta$．
作 $\triangle{ABC}$ 的高 $AD$，垂足为 $D$，则\[\begin{split}\dfrac{S_{\triangle{ABX}}}{S_{\triangle{ACY}}}&=\dfrac{\dfrac 12 AB\cdot AX\cdot \sin \alpha}{\dfrac 12\cdot AC\cdot AY\cdot \sin \alpha}\\&=\dfrac{\dfrac 12 BX\cdot AD}{\dfrac 12 CY\cdot AD}.\end{split}\]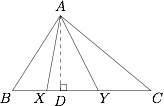
由此得$$\dfrac{AB\cdot AX}{AC\cdot AY}=\dfrac{BX}{CY}\cdots {\text{ ① }}$$同理$$\dfrac{AB\cdot AY}{AC\cdot AX}=\dfrac{BY}{CX}\cdots {\text{ ② }}$$由 ① $\times $ ② 得$$\dfrac{AB^2}{AC^2}=\dfrac{BX\cdot BY}{CY\cdot CX},$$变形整理即得$$AB^2\cdot CY\cdot CX=AC^2\cdot BX\cdot BY.$$因此充分性得证．
必要性：
作 $\triangle{ABC}$ 的高 $AD$，垂足为 $D$，不妨设 $\angle{BAX}=\alpha$，$\angle{CAY}=\beta$，$\angle{XAY}=\theta$，则$$\dfrac{S_{\triangle{ABX}}}{S_{\triangle{ACY}}}=\dfrac{\dfrac 12AB\cdot AX\cdot \sin \alpha}{\dfrac 12\cdot AC\cdot AY\cdot \sin \beta}=\dfrac{\dfrac 12 BX\cdot AD}{\dfrac 12 CY\cdot AD},$$所以$$\dfrac{AB\cdot AX\cdot \sin \alpha}{AC\cdot AY\cdot \sin \beta}=\dfrac{BX}{CY}\cdots {\text{ ③ }}$$同理$$\dfrac{AB\cdot AY\cdot \sin{\alpha+\theta}}{AC\cdot AX\cdot \sin(\beta+\theta)}=\dfrac{BY}{CX}\cdots {\text{ ④ }}$$由 ③ $\times$ ④ 得$$\dfrac{AB^2\cdot \sin \alpha\cdot \sin(\alpha+\theta)}{AC^2\cdot \sin \beta\cdot \sin(\beta+\theta)}=\dfrac{BX\cdot BY}{CY\cdot CX},$$由题设得$$\dfrac{BX\cdot BY}{CX\cdot CY}=\dfrac{AB^2}{AC^2},$$两式联立得$$\sin \alpha \sin(\alpha+\theta)=\sin\beta\sin(\beta+\theta),$$即$$\sin \alpha(\sin \alpha\cos \theta+\cos \alpha \sin \theta)=\sin \beta (\sin \beta \cos \theta+\cos \beta \sin \theta),$$利用二倍角公式及和差化积公式整理可得$$\sin(\alpha -\beta)[\sin(\alpha +\beta)\cos \theta +\cos( \alpha+\beta)\sin \theta ]=0,$$即$$\sin(\alpha -\beta)\sin(\alpha+\beta+\theta)=0.$$因为$$\alpha +\beta +\theta =\angle{BAC},$$且 $\angle{BAC}$ 是 $\triangle{ABC}$ 的一个内角，所以$$\sin(\alpha -\beta)=0,$$故 $\alpha =\beta$，因此 $\angle{BAX}=\angle{CAY}$．
若 $\angle{BAX}=\angle{CAY}$，设 $\angle{BAX}=\angle{CAY}=\alpha$，$\angle{XAY}=\theta$．
作 $\triangle{ABC}$ 的高 $AD$，垂足为 $D$，则\[\begin{split}\dfrac{S_{\triangle{ABX}}}{S_{\triangle{ACY}}}&=\dfrac{\dfrac 12 AB\cdot AX\cdot \sin \alpha}{\dfrac 12\cdot AC\cdot AY\cdot \sin \alpha}\\&=\dfrac{\dfrac 12 BX\cdot AD}{\dfrac 12 CY\cdot AD}.\end{split}\]
由此得$$\dfrac{AB\cdot AX}{AC\cdot AY}=\dfrac{BX}{CY}\cdots {\text{ ① }}$$同理$$\dfrac{AB\cdot AY}{AC\cdot AX}=\dfrac{BY}{CX}\cdots {\text{ ② }}$$由 ① $\times $ ② 得$$\dfrac{AB^2}{AC^2}=\dfrac{BX\cdot BY}{CY\cdot CX},$$变形整理即得$$AB^2\cdot CY\cdot CX=AC^2\cdot BX\cdot BY.$$因此充分性得证．必要性：
作 $\triangle{ABC}$ 的高 $AD$，垂足为 $D$，不妨设 $\angle{BAX}=\alpha$，$\angle{CAY}=\beta$，$\angle{XAY}=\theta$，则$$\dfrac{S_{\triangle{ABX}}}{S_{\triangle{ACY}}}=\dfrac{\dfrac 12AB\cdot AX\cdot \sin \alpha}{\dfrac 12\cdot AC\cdot AY\cdot \sin \beta}=\dfrac{\dfrac 12 BX\cdot AD}{\dfrac 12 CY\cdot AD},$$所以$$\dfrac{AB\cdot AX\cdot \sin \alpha}{AC\cdot AY\cdot \sin \beta}=\dfrac{BX}{CY}\cdots {\text{ ③ }}$$同理$$\dfrac{AB\cdot AY\cdot \sin{\alpha+\theta}}{AC\cdot AX\cdot \sin(\beta+\theta)}=\dfrac{BY}{CX}\cdots {\text{ ④ }}$$由 ③ $\times$ ④ 得$$\dfrac{AB^2\cdot \sin \alpha\cdot \sin(\alpha+\theta)}{AC^2\cdot \sin \beta\cdot \sin(\beta+\theta)}=\dfrac{BX\cdot BY}{CY\cdot CX},$$由题设得$$\dfrac{BX\cdot BY}{CX\cdot CY}=\dfrac{AB^2}{AC^2},$$两式联立得$$\sin \alpha \sin(\alpha+\theta)=\sin\beta\sin(\beta+\theta),$$即$$\sin \alpha(\sin \alpha\cos \theta+\cos \alpha \sin \theta)=\sin \beta (\sin \beta \cos \theta+\cos \beta \sin \theta),$$利用二倍角公式及和差化积公式整理可得$$\sin(\alpha -\beta)[\sin(\alpha +\beta)\cos \theta +\cos( \alpha+\beta)\sin \theta ]=0,$$即$$\sin(\alpha -\beta)\sin(\alpha+\beta+\theta)=0.$$因为$$\alpha +\beta +\theta =\angle{BAC},$$且 $\angle{BAC}$ 是 $\triangle{ABC}$ 的一个内角，所以$$\sin(\alpha -\beta)=0,$$故 $\alpha =\beta$，因此 $\angle{BAX}=\angle{CAY}$．
答案
解析
备注
