如图，锐角 $\triangle ABC$ 中，$AB<AC$，且点 $D$ 和 $E$ 在边 $BC$ 上，满足 $BD=CE$．若在 $\triangle ABC$ 内存在点 $P$ 满足 $PD\parallel AE$ 且 $\angle PAB=\angle EAC$，证明：$\angle PBA=\angle PCA$．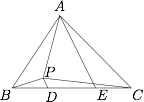
【难度】
【出处】
2013年全国高中数学联赛辽宁省预赛
【标注】
【答案】
略
【解析】
如图，作平行四边形 $ABFC$ 和平行四边形 $ABGP$，则$$AC=FB,\angle ACE=\angle FBD,$$又 $BD=CE$，故$$\triangle AEC\cong\triangle FDB,$$所以$$\angle BDF=\angle AEC,$$故 $FD\parallel AE$．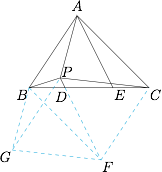
又 $PD\parallel AE$，故 $P,D,F$ 三点共线，因此\[\angle BFP=\angle BFD=\angle EAC=\angle BAP=\angle BGP,\]故 $B,G,F,P$ 四点共圆，所以$$\angle FBG=\angle FPG=\angle BAP+\angle EAP=\angle CAP.$$又由于 $AP=BG$，$AC=BF$，所以$$\triangle APC\cong\triangle BGF,$$故 $\angle ABP=\angle BPG=\angle BFG=\angle ACP$．
又 $PD\parallel AE$，故 $P,D,F$ 三点共线，因此\[\angle BFP=\angle BFD=\angle EAC=\angle BAP=\angle BGP,\]故 $B,G,F,P$ 四点共圆，所以$$\angle FBG=\angle FPG=\angle BAP+\angle EAP=\angle CAP.$$又由于 $AP=BG$，$AC=BF$，所以$$\triangle APC\cong\triangle BGF,$$故 $\angle ABP=\angle BPG=\angle BFG=\angle ACP$．
答案
解析
备注
