如图，$AB,AC$ 是圆 $O$ 的两条割线，分别交圆 $O$ 于另两点 $E,D$，又 $M,N$ 分别是 $EB,DC$ 的中点．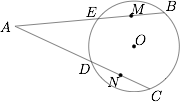
【难度】
【出处】
2011年全国高中数学联赛新疆维吾尔族自治区预赛
【标注】
-
求证 $A,M,O,N$ 四点共圆；标注答案略解析连接 $AO,OM,ON,MN$．
因为 $M,N$ 分别是弦 $EB,DC$ 的中点，所以$$\angle{AMO}=\angle{ANO}=90^{\circ},$$故四边形 $AMON$ 是 $AO$ 为直径的圆内接四边形，所以 $A,M,O,N$ 四点共圆． -
求 $\angle{AMN}+\angle{OAC}$ 的值．标注答案$90^{\circ}$解析由 $A,M,O,N$ 四点共圆知$$\angle{OAN}=\angle{OMN},$$所以$$\angle{AMN}+\angle{OAN}=\angle{AMN}+\angle{OMN}=\angle{OMA}=90^{\circ}.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
