如图，$P,Q$ 分别是圆内接四边形 $ABCD$ 的对角线 $AC,BD$ 的中点．若 $\angle{BPA}=\angle{DPA}$，证明：$\angle{AQB}=\angle{CQB}$．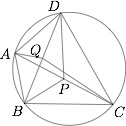
【难度】
【出处】
2011年全国高中数学联赛（二试）
【标注】
【答案】
略
【解析】
延长线段 $DP$ 与圆交于另一点 $E$，则$$\angle{CPE}=\angle{DPA}=\angle{BPA}.$$
因为 $P$ 是线段 $AC$ 的中点，故 $\widehat{AB}=\widehat{CE}$，从而$$\angle{CDP}=\angle{BDA}.$$又 $\angle{ABD}=\angle{PCD}$，所以$$\triangle{ABD}\backsim \triangle{PCD},$$于是$$\dfrac{AB}{BD}=\dfrac{PC}{CD},$$即$$AB\cdot CD=PC\cdot BD,$$从而有\[\begin{split}AB\cdot CD&=\dfrac 12 AC\cdot BD\\&=AC\cdot \left(\dfrac 12 BD\right)\\&=AC\cdot BQ,\end{split}\]又 $\angle{ABQ}=\angle{ACD}$，所以 $\triangle{ABQ}\backsim \triangle{ACD}$，故$$\angle{QAB}=\angle{DAC}.$$延长线段 $AQ$ 与圆交于另一点 $F$，则 $\angle{CAB}=\angle{DAF}$，故$$\widehat{BC}=\widehat{DF}.$$又因为 $Q$ 为 $BD$ 的中点，所以$$\angle{CQB}=\angle{DQF},$$而 $\angle{AQB}=\angle{DQF}$，所以$$\angle{AQB}=\angle{CQB}.$$
因为 $P$ 是线段 $AC$ 的中点，故 $\widehat{AB}=\widehat{CE}$，从而$$\angle{CDP}=\angle{BDA}.$$又 $\angle{ABD}=\angle{PCD}$，所以$$\triangle{ABD}\backsim \triangle{PCD},$$于是$$\dfrac{AB}{BD}=\dfrac{PC}{CD},$$即$$AB\cdot CD=PC\cdot BD,$$从而有\[\begin{split}AB\cdot CD&=\dfrac 12 AC\cdot BD\\&=AC\cdot \left(\dfrac 12 BD\right)\\&=AC\cdot BQ,\end{split}\]又 $\angle{ABQ}=\angle{ACD}$，所以 $\triangle{ABQ}\backsim \triangle{ACD}$，故$$\angle{QAB}=\angle{DAC}.$$延长线段 $AQ$ 与圆交于另一点 $F$，则 $\angle{CAB}=\angle{DAF}$，故$$\widehat{BC}=\widehat{DF}.$$又因为 $Q$ 为 $BD$ 的中点，所以$$\angle{CQB}=\angle{DQF},$$而 $\angle{AQB}=\angle{DQF}$，所以$$\angle{AQB}=\angle{CQB}.$$
答案
解析
备注
