设椭圆 $\dfrac {x^2}{a^2}+\dfrac {y^2}3=1(a>\sqrt 3)$ 的右焦点为 $F$，右顶点为 $A$，已知 $\dfrac 1{|OF|}+\dfrac 1{|OA|}=\dfrac {3e}{|FA|}$，其中 $O$ 为原点，$e$ 为椭圆的离心率．
【难度】
【出处】
2016年高考天津卷（文）
【标注】
-
求椭圆的方程；标注答案$\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$解析由 $\dfrac {1}{\left|OF\right|}+\dfrac {1}{\left|OA\right|}=\dfrac {3e}{\left|FA\right|}$ 可知$$\dfrac{1}{c }+\dfrac{1}{a}=\dfrac{3\cdot\dfrac{c}{a} }{a-c}, $$解得 $a=2$．
故椭圆方程为 $\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$． -
设过点 $A$ 的直线 $l$ 与椭圆交于点 $B$（$B$ 不在 $x$ 轴上），垂直于 $l$ 的直线与 $l$ 交于点 $M$，与 $y$ 轴交于点 $H$．若 $BF\perp HF$，且 $\angle MOA=\angle MAO$，求直线 $l$ 的斜率．标注答案$\pm \dfrac{\sqrt{6} }{4} $解析如图，设 $B$ 点坐标为 $\left(2\cos\theta,\sqrt{3}\sin\theta \right) $，其中 $\sin\theta\ne 0$，$H$ 点坐标为 $\left(0,h\right) $．
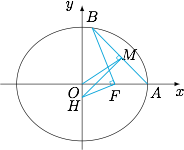因为 $BF \perp HF$，故 $\overrightarrow{FB}\cdot\overrightarrow{FH}=0$，解得$$h=\dfrac{2\cos\theta-1}{\sqrt{3}\sin\theta }.$$因为 $M$ 点在直线 $l$ 上，所以可以设 $M$ 点坐标为 $\left(m,\dfrac{\sqrt{3}(m-2)\sin\theta }{2\cos\theta-2} \right) $．
由题意，$HM\perp AB$，所以\[\begin{split}\overrightarrow{HM}\cdot\overrightarrow{AB}&=\left(m,\dfrac{\sqrt{3}(m-2)\sin\theta }{2\cos\theta-2}-\dfrac{2\cos\theta-1}{\sqrt{3}\sin\theta }\right)\cdot\left(2\cos\theta-2,\sqrt{3}\sin\theta \right) \\&= \left(\dfrac{1}{2}\cos\theta-\dfrac{7}{2} \right)m+4+\cos\theta \\&=0,\end{split}\]故$$m=\dfrac{8+2\cos\theta}{7-\cos\theta}.$$因为 $\angle MOA= \angle MAO$，所以 $m = 1$，解得 $\cos\theta = -\dfrac{1}{3} $，从而 $M\left(1,\pm\dfrac{\sqrt 6}4\right)$，所以直线 $l$ 的斜率为 $\pm \dfrac{\sqrt{6} }{4} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
