在棱长为 $a$ 的正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，$E,F,M$ 分别是 $AB,B{B_1},{A_1}{D_1}$ 的中点．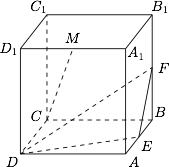
【难度】
【出处】
2007年武汉大学自主招生保送生测试
【标注】
-
求证：$CM \perp DEF$；标注答案略解析在平面 $AD_1$ 上，过 $M$ 作 $AD$ 的垂线，垂足为 $H$，连接 $A_1B$，如图．
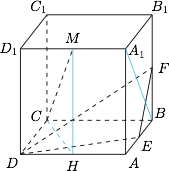根据三垂线定理，有\[\left.\begin{split} \left.\begin{split}MH\perp ABCD,\\ CH\perp DE,\end{split}\right\}\Rightarrow CM\perp DE,\\
\left.\begin{split}CB,MA_1\perp ABB_1A_1, \\ A_1B\perp EF ,\end{split}\right\}\Rightarrow CM\perp EF,\end{split}\right\}\Rightarrow CM\perp DEF.\] -
求点 $M$ 到平面 $DEF$ 的距离．标注答案$\dfrac{5}{6}a$解析如图，连接 $MD,ME,MF$，延长 $A_1A$ 到 $N$，使得 $AN=\dfrac 12AA_1$，连接 $EN$．
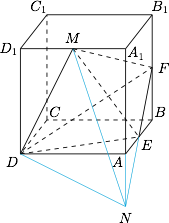用等体积法，有\[M-DEF=E-DFM=\dfrac 12N-DFM=\dfrac 12F-DMN=\dfrac{5a^3}{48},\]而 $DE=\dfrac{\sqrt 5}2a$，$EF=\dfrac{\sqrt 2}2a$，$DF=\dfrac 32a$，于是\[\cos \angle DEF=\dfrac{DE^2+EF^2-DF^2}{2\cdot DE\cdot EF}=-\dfrac{1}{\sqrt{10}},\]进而\[\triangle DEF=\dfrac 12\cdot \sin\angle DEF\cdot DE\cdot FE=\dfrac 38a^2,\]因此\[d(M,DEF)=\dfrac {3M-DEF}{\triangle DEF}=\dfrac 56a.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
