如图，在五边形 $ABCDE$ 中，$BC \parallel AE$，$AB=BC+AE$，$\angle ABC=\angle CDE$，$M$ 为 $CE$ 中点，$O$ 为 $\triangle BCD$ 的外心，且 $OM\perp MD$．延长 $DM$ 至点 $K$，使得 $MK=MD$．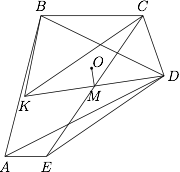
【难度】
【出处】
2014年全国高中数学联赛福建省预赛
【标注】
-
求证：$\angle BKC=\angle BDC$；标注答案略解析因为 $M$ 为 $KD$ 的中点，且 $OM\perp MD$，所以 $OK=OD$，点 $K$ 在 $\triangle BCD$ 的外接圆上．因此 $\angle BKC=\angle BDC $．
-
求证：$\angle ABC=2\angle BDA$．标注答案略解析延长 $AE$ 至点 $T$，使得$$ET=BC.$$连结 $TB$，$TC$，$TD$，$TK$，$KE$．
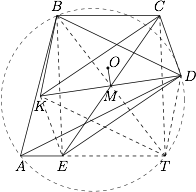由 $AB=BC+AE$ 知，$$AT=AB.$$又 $BC \parallel AE$，所以$$\angle CBT=\angle BTA=\angle ABT,\angle ABC=2\angle BTA,$$所以四边形 $BCTE$ 为平行四边形，故 $M$ 也是 $BT$ 中点．
从而四边形 $BKTD$ 为平行四边形，所以$$\angle BKD=\angle KDT.$$而四边形 $KCDE$ 为平行四边形，所以$$\angle CKD=\angle KDE.$$故有$$\angle BKC=\angle BKD- \angle CKD=\angle KDT - \angle KDE=\angle EDT,$$所以$$\angle BDC=\angle BKC=\angle EDT,$$则$$\angle BDT=\angle BDE+ \angle EDT=\angle BDE + \angle BDC=\angle CDE=\angle ABC.$$所以$$\angle BDT+\angle BAT=\angle ABC + \angle BAT=180^{\circ}.$$因此 $B$，$A$，$T$，$D$ 四点共圆，所以$$\angle BDA=\angle BTA, \angle ABC=2\angle BTA =2\angle BDA.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
