是否存在三边为连续自然数的三角形，使得
【难度】
【出处】
2005年上海交通大学保送推优生考试
【标注】
-
最大角是最小角的两倍，若存在，求出该三角形；若不存在，请说明理由．标注答案存在这样的三角形，三边长分别为 $4,5,6$解析如图．
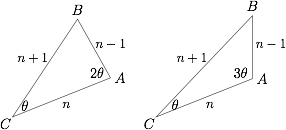不妨设 $\triangle ABC$ 中，$A$ 为最大角，$C$ 为最小角，则 $BC = n + 1$，$AB = n - 1$，$AC = n$，其中 $n$ 是自然数，则$$\left( {n - 1} \right) + n > n + 1,n > 2,$$即 $n \geqslant 3$．
若 $A = 2\theta $，$C = \theta $，则由正弦定理，有$$\dfrac{{n + 1}}{{\sin 2\theta }} = \dfrac{{n - 1}}{{\sin \theta }},$$所以$$\cos \theta = \dfrac{1}{2} \cdot \dfrac{{n + 1}}{{n - 1}},$$又$$\cos \theta = \dfrac{{{n^2} + {{\left( {n + 1} \right)}^2} - {{\left( {n - 1} \right)}^2}}}{{2n\left( {n + 1} \right)}} = \dfrac{{n + 4}}{{2\left( {n + 1} \right)}},$$于是$$\dfrac{1}{2} \cdot \dfrac{{n + 1}}{{n - 1}} = \dfrac{{n + 4}}{{2\left( {n + 1} \right)}},$$解得 $n = 5$．所以存在这样的三角形，三边长分别为 $4,5,6$． -
最大角是最小角的三倍，若存在，求出该三角形；若不存在，请说明理由．标注答案不存在解析若 $A = 3\theta $，$C = \theta $，则由正弦定理，有$$\dfrac{{n - 1}}{{\sin \theta }} = \dfrac{{n + 1}}{{\sin 3\theta }},$$得$$ 3 - 4{\sin ^2}\theta = \dfrac{{n + 1}}{{n - 1}},$$所以$${\cos ^2}\theta = \dfrac{n}{{2\left( {n - 1} \right)}},$$又$$\cos \theta = \dfrac{{n + 4}}{{2\left( {n + 1} \right)}},$$所以$${\left( {\dfrac{{n + 4}}{{2\left( {n + 1} \right)}}} \right)^2} = \dfrac{n}{{2\left( {n - 1} \right)}},$$即$${n^3} - 3{n^2} - 6n + 16 = 0,$$也即$$\left( {n - 2} \right)\left( {{n^2} - n - 8} \right) = 0,$$此方程无符合 $n \geqslant 3$ 的自然数解，所以不存在这样的三角形．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
