设 $A,B,C$ 为边长为 $1$ 的三角形三边上各一点,求:$A{B^2} + B{C^2} + C{A^2}$ 的最小值.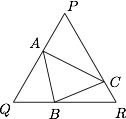

【难度】
【出处】
2012年北京大学等十三校联考自主招生
【标注】
【答案】
$\dfrac{3}{4}$
【解析】
设 $PA = a$,$QB = b$,$RC = c$,则$$A{B^2} = {\left( {1 - a} \right)^2} + {b^2} - \left( {1 - a} \right)b \geqslant \dfrac{{{{\left( {1 - a} \right)}^2} + {b^2}}}{2},$$当且仅当 $1 - a = b$ 时取等号.$$B{C^2} = {\left( {1 - b} \right)^2} + {c^2} - \left( {1 - b} \right)c \geqslant \dfrac{{{{\left( {1 - b} \right)}^2} + {c^2}}}{2}$$当且仅当 $1 - b = c$ 时取等号.$$C{A^2} = {\left( {1 - c} \right)^2} + {a^2} - \left( {1 - c} \right)a \geqslant \dfrac{{{{\left( {1 - c} \right)}^2} + {a^2}}}{2}$$当且仅当 $1 - c = a$ 时取等号.
于是$$A{B^2} + B{C^2} + C{A^2} \geqslant \dfrac{{{{\left( {1 - a}\right)}^2} + {a^2} + {{\left( {1 - b} \right)}^2} + {b^2} + {{\left( {1 - c} \right)}^2} + {c^2}}}{2} \geqslant \dfrac{3}{4},$$当且仅当 $a = b = c = \dfrac{1}{2}$ 时同时取得等号.
因此 $A{B^2} + B{C^2} + C{A^2}$ 的最小值为 $\dfrac{3}{4}$.
于是$$A{B^2} + B{C^2} + C{A^2} \geqslant \dfrac{{{{\left( {1 - a}\right)}^2} + {a^2} + {{\left( {1 - b} \right)}^2} + {b^2} + {{\left( {1 - c} \right)}^2} + {c^2}}}{2} \geqslant \dfrac{3}{4},$$当且仅当 $a = b = c = \dfrac{1}{2}$ 时同时取得等号.
因此 $A{B^2} + B{C^2} + C{A^2}$ 的最小值为 $\dfrac{3}{4}$.
答案
解析
备注