设直线 $x+y=1$ 与抛物线 $y^{2}=2px(p>0)$ 相交于点 $A,B$,若 $OA\perp OB$,求抛物线方程以及 $\triangle OAB$ 的面积.
【难度】
【出处】
2013年全国高中数学联赛江西省预赛
【标注】
【答案】
$y^2=x$,$\dfrac{\sqrt 5}{2}$
【解析】
设焦点 $A(x_{1},y_{1})$,$B(x_{2},y_{2})$.
由 $y^{2}=2px$ 与 $x+y=1$,得$$y^{2}+2py-2p=0,$$故有\[x_{1}=1+p-\sqrt{p^{2}+2p},y_{1}=-p+\sqrt{p^{2}+2p},\]以及\[x_{2}=1+p+\sqrt{p^{2}+2p},y_{2}=-p-\sqrt{p^{2}+2p}.\]因为 $OA\perp OB$,即 $\overrightarrow{OA}\cdot \overrightarrow{OB}=0$,所以$$x_{1}x_{2}+y_{1}y_{2}=0,$$即\[[(1+p)^{2}-(p^{2}+2p)]+[p^{2}-(p^{2}+2p)]=0,\]化简得$$1-2p=0,$$因此抛物线方程为 $y^{2}=x$,从而交点 $A,B$ 坐标为:$A\left(\dfrac{3-\sqrt 5}{2},\dfrac{-1+\sqrt 5}{2}\right)$,$B\left(\dfrac{3+\sqrt 5}{2},\dfrac{-1-\sqrt 5}{2}\right)$,因此\[OA^{2}=x_{1}^{2}+y_{1}^{2}=5-2\sqrt 5, OB^{2}=x_{2}^{2}+y_{2}^{2}=5+2\sqrt 5,\]故$$S_{\triangle OAB}=\dfrac{1}{2}\cdot |OA|\cdot |OB|=\dfrac{\sqrt 5}{2}.$$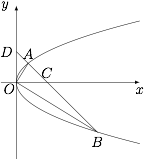
由 $y^{2}=2px$ 与 $x+y=1$,得$$y^{2}+2py-2p=0,$$故有\[x_{1}=1+p-\sqrt{p^{2}+2p},y_{1}=-p+\sqrt{p^{2}+2p},\]以及\[x_{2}=1+p+\sqrt{p^{2}+2p},y_{2}=-p-\sqrt{p^{2}+2p}.\]因为 $OA\perp OB$,即 $\overrightarrow{OA}\cdot \overrightarrow{OB}=0$,所以$$x_{1}x_{2}+y_{1}y_{2}=0,$$即\[[(1+p)^{2}-(p^{2}+2p)]+[p^{2}-(p^{2}+2p)]=0,\]化简得$$1-2p=0,$$因此抛物线方程为 $y^{2}=x$,从而交点 $A,B$ 坐标为:$A\left(\dfrac{3-\sqrt 5}{2},\dfrac{-1+\sqrt 5}{2}\right)$,$B\left(\dfrac{3+\sqrt 5}{2},\dfrac{-1-\sqrt 5}{2}\right)$,因此\[OA^{2}=x_{1}^{2}+y_{1}^{2}=5-2\sqrt 5, OB^{2}=x_{2}^{2}+y_{2}^{2}=5+2\sqrt 5,\]故$$S_{\triangle OAB}=\dfrac{1}{2}\cdot |OA|\cdot |OB|=\dfrac{\sqrt 5}{2}.$$

答案
解析
备注