如图,四边形 $ABCD$ 中,$E,F$ 分别是 $AD,BC$ 的中点,$P$ 是对角线 $BD$ 上的一点;直线 $EP,PF$ 分别交 $AB,DC$ 的延长线于 $M,N$.证明:线段 $MN$ 被直线 $EF$ 所平分.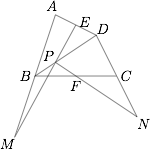

【难度】
【出处】
2013年全国高中数学联赛江西省预赛
【标注】
【答案】
略
【解析】
设 $EF$ 交 $MN$ 于 $G$,直线 $EF$ 截 $\triangle PMN$,则\[\dfrac{NG}{GM}\cdot \dfrac{ME}{EP}\cdot \dfrac{PF}{FN}=1.\]为证 $G$ 是线段 $MN$ 的中点,只要证,\[\dfrac{PF}{NF}=\dfrac{PE}{ME}.\cdots\cdots \text{ ① }\]直线 $AB$ 截 $\triangle PDE$,得\[\dfrac{PN}{NF}\cdot \dfrac{FC}{CB}\cdot \dfrac{DB}{BP}=1,\cdots\cdots\text{ ② }\]即\[\dfrac{NP}{2NF}=\dfrac{PD}{BD}\cdots\cdots\text{ ③ }\]②③ 相加得$$\dfrac{MP}{ME}+\dfrac{NP}{NF}=2,$$即$$\dfrac{NP}{NF}-1=1-\dfrac{MP}{ME},$$也即$$\dfrac{PF}{NF}=\dfrac{PE}{ME},$$因此结论得证.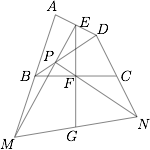

答案
解析
备注