如图,在平面直角坐标系中,方程为 $x^2+y^2+Dx+Ey+F=0$ 的圆 $M$ 的内接四边形 $ABCD$ 的对角线 $AC$ 和 $BD$ 互相垂直,且 $AC$ 和 $BD$ 分别在 $x$ 轴和 $y$ 轴上.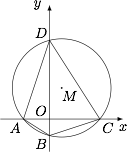

【难度】
【出处】
2012年全国高中数学联赛河北省预赛(高二)
【标注】
-
求证:$F<0$;标注答案略解析由题意,原点 $O$ 必定在圆 $M$ 内,即若将点 $(0,0)$ 代入方程$$x^2+y^2+Dx+Ey+F=0,$$则其左边的值小于 $0$,于是有 $F<0$.
-
若四边形 $ABCD$ 的面积为 $8$,对角线 $AC$ 的长为 $2$,且 $\overrightarrow{AB}\cdot\overrightarrow{AD}=0$,求 $D^2+E^2-4F$ 的值.标注答案$64$解析对角线互相垂直的四边形 $ABCD$ 的面积$$S=\dfrac{|AC|\cdot|BD|}{2},$$因为$$S=8,|AC|=2,$$所以 $|BD|=8$.
又因为$$\overrightarrow{AB}\cdot\overrightarrow{AD}=0,$$所以 $\angle A$ 为直角,于是$$|BD|=2r=8,$$故 $r=4$.
对于方程 $x^2+y^2+Dx+Ey+F=0$ 所表示的圆,可知$$\dfrac{D^2}{4}+\dfrac{E^2}{4}-F=r^2,$$所以$$D^2+E^2-4F=4r^2=64.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2