已知 $C,D$ 是以 $AB$ 为直径的半圆 $O$ 上的两个点,弦 $AD,BC$ 交于点 $E$,$F,G$ 分别是 $AC,BD$ 延长线上的点,且满足 $AF\cdot BG=AE\cdot BE$,若 $\triangle{AEF},\triangle{BEG}$ 的垂心分别为 $H_1,H_2$,证明:
【难度】
【出处】
2009年全国高中数学联赛天津市预赛
【标注】
-
$AH_1,BH_2$ 的交点 $K$ 在圆 $O$ 上;标注答案略解析因为$$\angle{CAD}=\angle{CBD},\dfrac{AF}{AE}=\dfrac{BE}{BG},$$所以$$\triangle{AEF}\backsim \triangle{BGE}.$$又因为$$BC\perp AF,AD\perp BG,$$所以$$\angle{CEF}+\angle{BEG}=\angle{CEF}+\angle{CFE}=90^{\circ},$$于是有 $\angle{FEG}=90^{\circ}$.
设 $AK,BK$ 分别与 $EF,EG$ 交于点 $M,N$,则四边形 $MENK$ 为矩形,因此$$\angle{AKB}=90^{\circ},$$即 $K$ 在圆 $O$ 上.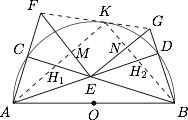
-
$F,K,G$ 三点共线.标注答案略解析因为 $AM,BN$ 分别是相似 $\triangle{AEF}$ 与 $\triangle{BGE}$ 对应边上的高线,所以有$$\dfrac{GN}{NE}=\dfrac{EM}{MF}.$$又因为$$NE=MK,EM=NK,$$所以$$\dfrac{GN}{MK}=\dfrac{NK}{MF}.$$由于$$\angle{FMK}=\angle{KNG}=90^{\circ},$$因此有$$\triangle{MFK}\cong \triangle{NKG},$$于是可得$$\angle{FKM}+\angle{GKN}=\angle{FKM}+\angle{KFM}=90^{\circ},$$即$$\angle{FKM}+\angle{GKN}+\angle{MKN}=180^{\circ},$$从而有 $F,K,G$ 三点共线.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2