边长为 $3$ 的菱形 $A_1BCD$ 中，$\angle{A_1}=60^{\circ}$，$E$ 为线段 $A_1B$ 上一动点（除去点 $A_1,B$ 外），以 $DE$ 为折痕，将 $\triangle{A_1DE}$ 折起，使二面角 $A-DE-C$ 成 $60^{\circ}$，如图．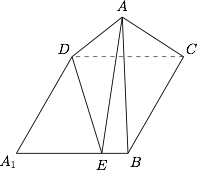
【难度】
【出处】
2009年全国高中数学联赛河北省预赛
【标注】
-
求证：$A$ 点在面 $DEBC$ 上的射影 $O$ 不可能为 $\triangle{DBC}$ 的垂心；标注答案略解析假设 $O$ 为 $\triangle{DBC}$ 的垂心．
因为 $\triangle{DBC}$ 为正三角形，所以$$AB=AC=AD=3.$$因为$$AE+EB=3=AB,$$所以 $AB,BE,EA$ 三线段不可能构成三角形，矛盾，故假设不成立．
因此 $A$ 点在面 $DEBC$ 上的射影 $O$ 不可能为 $\triangle{DBC}$ 的垂心． -
当 $A_1E=2EB$ 时，求直线 $BC$ 与面 $ADE$ 所成的角．标注答案$\arcsin{\dfrac{3\sqrt 7}{14}}$解析过点 $O$ 作 $ON\perp DE$，垂足为 $N$，连接 $AN$．
因为 $AO\perp$ 面 $DEC$，则有 $AN\perp DE$，所以 $\angle{ANO}$ 是二面角 $A-DE-C$ 的平面角．
延长 $DE,CB$ 交于点 $M$，连接 $AM$，则 $AM$ 为面 $ADE$ 与面 $ABC$ 的交线．
因为 $BE\parallel CD$，且 $BE=\dfrac 13 CD$，所以$$MB=\dfrac 32,MC=\dfrac 92.$$过点 $C$ 作面 $DAE$ 的垂线，垂足为 $H$，连接 $MH$，则 $\angle{HMC}$ 为直线 $BC$ 与面 $ADE$ 所成的角．
在 $\triangle{ADE}$ 中，\[\begin{split}DE^2&=AD^2+AE^2-2AD\cdot AE\cdot \cos 60^{\circ}\\&=9+4-2\cdot 3\cdot 2\cdot \dfrac 12 \\&=7,\end{split}\]所以 $DE=\sqrt 7$，于是$$S_{\triangle{ADE}}=\dfrac{3\sqrt 3}{2}=\dfrac 12 \cdot DE\cdot AN=\dfrac {\sqrt 7}{2}AN,$$所以$$AN=\dfrac{3\sqrt{21}}{7},AO=AN\cdot \sin 60^{\circ}=\dfrac{9\sqrt 7 }{14}.$$又因为$$S_{\triangle{DCE}}=\dfrac 12 \cdot DC\cdot A_1D \sin 60^{\circ}=\dfrac{9\sqrt 3}{4},$$且 $V_{A-DCE}=V_{C-ADE}$，所以$$\dfrac 13 S_{\triangle{DCE}}\cdot AO=\dfrac 13 S_{\triangle{ADE}}\cdot CH,$$即$$\dfrac 13 \cdot \dfrac{9\sqrt 3}{4}\cdot \dfrac{9\sqrt 7}{14}=\dfrac 13 \cdot \dfrac{3\sqrt 3}{2}\cdot CH,$$故 $CH=\dfrac{27\sqrt 7}{28}$．
在 $\triangle{CHM}$ 中，$$\sin {\angle{HMC}}=\dfrac{CH}{MC}=\dfrac{3\sqrt 7}{14},$$故直线 $BC$ 与面 $ADE$ 所成的角为 $\angle{HMC}=\arcsin{\dfrac{3\sqrt 7}{14}}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
