如图，已知 $\odot O_1$ 与 $\odot O_2$ 外切于点 $P$，$\odot O_2$ 与 $\odot O $ 内切于点 $Q$，线段 $O_1O_2$ 与 $PQ$ 交于点 $G$，过 $G$ 作 $\odot O_1$ 的切线 $GN$，切点为 $N$．求证：直线 $NG$ 与 $\odot O_2$ 也相切．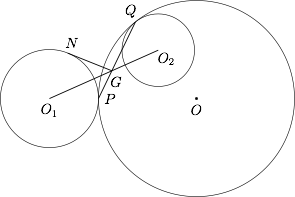
【难度】
【出处】
2014年全国高中数学联赛江苏省复赛（二试）
【标注】
【答案】
略
【解析】
过 $G$ 作 $\odot O_2$ 的切线 $GM$，切点为 $M$，连结 $O_1O$，$OQ$，$O_1N$，$O_2M$，则点 $P$ 在 $O_1O$ 上，点 $O_2$ 在 $OQ$ 上．
过 $O_2$ 作 $O_2H \parallel PQ$ 交 $OO_1$ 于 $H$ 点．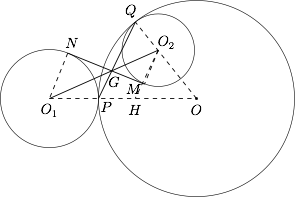
设 $\odot O_1$，$\odot O_2$，$\odot O $ 的半径分别为 $r_1$，$r_2$，$R$，则由 $O_2H \parallel PQ$ 得，$$PH=QO_2=r_2\text{且} \dfrac {O_1G}{O_2G}=\dfrac {O_1P}{PH}=\dfrac {r_1}{r_2},$$而$$\dfrac {O_1N}{O_2M}=\dfrac {r_1}{r_2},$$所以$$\dfrac {O_1G}{O_2G}=\dfrac {O_1N}{O_2M}.$$又 $GN$，$GM$ 分别为 $\odot O_1$，$\odot O_2$ 的切线，所以$$\angle O_1NG=90^{\circ}=\angle O_2MG,$$于是$$\mathrm {Rt}\triangle NO_1G \sim\mathrm {Rt}\triangle MO_2G,$$故$$\angle O_1GN=\angle O_2GM,$$从而有 $N$，$G$，$M$ 三点共线，即直线 $NG$ 与 $\odot O_2$ 也相切．
过 $O_2$ 作 $O_2H \parallel PQ$ 交 $OO_1$ 于 $H$ 点．
设 $\odot O_1$，$\odot O_2$，$\odot O $ 的半径分别为 $r_1$，$r_2$，$R$，则由 $O_2H \parallel PQ$ 得，$$PH=QO_2=r_2\text{且} \dfrac {O_1G}{O_2G}=\dfrac {O_1P}{PH}=\dfrac {r_1}{r_2},$$而$$\dfrac {O_1N}{O_2M}=\dfrac {r_1}{r_2},$$所以$$\dfrac {O_1G}{O_2G}=\dfrac {O_1N}{O_2M}.$$又 $GN$，$GM$ 分别为 $\odot O_1$，$\odot O_2$ 的切线，所以$$\angle O_1NG=90^{\circ}=\angle O_2MG,$$于是$$\mathrm {Rt}\triangle NO_1G \sim\mathrm {Rt}\triangle MO_2G,$$故$$\angle O_1GN=\angle O_2GM,$$从而有 $N$，$G$，$M$ 三点共线，即直线 $NG$ 与 $\odot O_2$ 也相切．
答案
解析
备注
