过直线 $x-2y+13=0$ 上一动点 $A$（$A$ 不在 $y$ 轴上）作抛物线 $y^2=8x$ 的两条切线，$M,N$ 为切点，直线 $AM,AN$ 分别与 $y$ 轴交于点 $B,C$．
【难度】
【出处】
2015年全国高中数学联赛湖北省预赛
【标注】
-
证明：直线 $MN$ 恒过一定点；标注答案略解析如图．
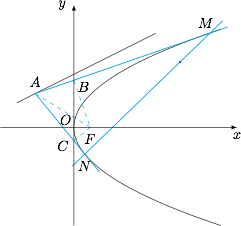设 $A(x_0,y_0),M(x_1,y_1),N(x_2,y_2)$，可知抛物线在点 $M$ 处的切线方程为$$AM:yy_1=4(x+x_1),$$又 $AM$ 过 $A(x_0,y_0)$，故$$y_0y_1=4(x_0+x_1)\qquad\qquad\cdots\cdots\text{ ① }$$容易知道 $\text{ ① }$ 式说明直线 $y_0y=4(x_0+x)$ 恒过点 $M(x_1,y_1)$．
同理可证得直线 $y_0y=4(x_0+x)$ 恒过点 $N(x_2,y_2)$．
因此直线 $MN$ 方程为$$y_0y=4(x_0+x),$$又$$x_0=2y_0-13,$$代入上式，得$$y_0(y-8)=4(x-13),$$所以直线 $MN$ 恒过定点 $(13,8)$． -
证明：$\triangle ABC$ 的外接圆恒过一定点，并求该圆半径的最小值．标注答案略解析直线 $AM$ 与 $y$ 轴交于点 $B\left(0,\dfrac{4x_1}{y_1}\right)$．
由于抛物线 $y^2=8x$ 的焦点为 $F(2,0)$，所以$$k_{BF}=\dfrac{\frac{4x_1}{y_1}-0}{0-2}=-\dfrac{2x_1}{y_1},$$又 $k_{BA}=\dfrac{4}{y_1}$，则$$k_{BA}\cdot k_{BF}=-\dfrac{8x_1}{y_1^2}=-1,$$所以 $BF\perp BA$．
同理可证 $CF\perp AC$．
因此 $A,B,C,F$ 四点共圆，且 $AF$ 为直径，因此 $\triangle ABC$ 的外接圆恒过定点 $F(2,0)$．
在 $AF$ 和直线 $x-2y+13=0$ 垂直时，圆的直径 $AF$ 最小，此时两直线联立，解得 $A(-1,6)$，则$$|AF|=3\sqrt5.$$因此 $\triangle ABC$ 的外接圆的半径的最小值为 $\dfrac{3\sqrt5}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
