如图,设 $S-ABCD$ 是一个高为 $3$ 的四棱锥,底面 $ABCD$ 是边长为 $2$ 的正方形,顶点 $S$ 在底面上的射影是正方形 $ABCD$ 的中心.$K$ 是棱 $SC$ 的中点,过 $AK$ 作平面与线段 $SB,SD$ 分别交于 $M,N$.($M,N$ 可以是线段的端点).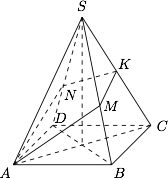

【难度】
【出处】
2012年全国高中数学联赛河北省预赛(高三)
【标注】
-
求直线 $AK$ 与平面 $SBC$ 所成角的正弦值;标注答案$\dfrac{2\sqrt{30}}{15}$解析设 $ AC\cap BD=O $,以 $ O $ 为坐标原点,$ OA $ 为 $ x $ 轴,$ OB $ 为 $ y $ 轴,$ OS $ 为 $ z $ 轴建立空间直角坐标系,则$$ A(\sqrt2,0,0),B(0,\sqrt2,0),C(-\sqrt2,0,0),S(0,0,3),$$所以$$ \overrightarrow{SB}=(0,\sqrt2,-3),\overrightarrow{SC}=(-\sqrt2,0,-3),K\left(-\dfrac{\sqrt2}{2},0,\dfrac32\right).$$设 $ \overrightarrow{m} $ 是平面 $ SBC $ 的一个法向量,易求得$$ \overrightarrow{m}=\left(-\dfrac{3}{\sqrt2},\dfrac{3}{\sqrt2},1\right).$$设 $ \theta $ 为 $ AK $ 与面 $ SBC $ 所成的角,因为$$ \overrightarrow{AK}=\left(-\dfrac{3\sqrt2}{2},0,\dfrac32\right),$$所以$$ \sin\theta=\left|\dfrac{\overrightarrow{m}\cdot\overrightarrow{AK}}{\left|\overrightarrow{m}\right|\cdot\left|\overrightarrow{AK}\right|}\right|=\dfrac{2\sqrt{30}}{15}.$$
-
求证:$\dfrac{V_{S-MKN}}{V_{S-BCD}}=\dfrac{SM\cdot SK\cdot SN}{SB\cdot SC\cdot SD}$,并求当 $M$ 是 $SB$ 中点时,四棱锥 $S-AMKN$ 的体积.标注答案$\dfrac32$解析设 $N,D$ 在平面 $SBC$ 的射影分别是 $H,H_1$,则$$\dfrac{NH}{DH_1}=\dfrac{SN}{SD}.$$因为$$\dfrac{S_{\triangle SMK}}{S_{\triangle SBC}}=\dfrac{SM\cdot SK}{SB\cdot SC},$$所以$$\dfrac{V_{S-MKN}}{V_{S-BCD}}=\dfrac{\frac13\cdot NH\cdot S_{\triangle SMK}}{\frac13\cdot DH_1\cdot S_{\triangle SBC}}=\dfrac{SM\cdot SK\cdot SN}{SB\cdot SC\cdot SD}.$$当 $M$ 是 $SB$ 的中点时,$$MK\parallel BC.$$因为 $BC\parallel\text{平面}SAD$,所以 $MK\parallel\text{平面}SAD$,所以$$MK\parallel AN,MK\parallel AD,$$故 $N,D$ 两点重合.
容易求得点 $M$ 到平面 $SAK$ 的距离为 $\dfrac{\sqrt2}{2}$,且$$S_{\triangle SAK}=\dfrac12S_{\triangle SAC}=\dfrac{3\sqrt2}{2},$$所以$$V_{S-AMKN}=\dfrac13\cdot S_{\triangle SAK}\cdot\sqrt2+\dfrac13\cdot S_{\triangle SAK}\cdot\dfrac{\sqrt2}{2}=\dfrac{\sqrt2}{2}\cdot S_{\triangle SAK}=\dfrac32.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2