已知 $O$ 为 $\triangle ABC$ 的内部一点，$\angle BAO =\angle CAO=\angle CBO=\angle ACO$，试探究 $\triangle ABC$ 的三边满足的关系，并证明你的结论．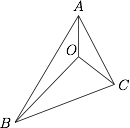
【难度】
【出处】
2014年湖南省高中数学竞赛
【标注】
【答案】
$BC^2=AB \cdot AC$
【解析】
$\triangle ABC$ 的三边满足的关系为 $BC^2=AB \cdot AC$，证明如下：
如图所示，延长 $AO$ 与 $\triangle BOC$ 的外接圆相交于点 $D$，连结 $BD$，$CD$，设$$\angle BAO =\angle CAO=\angle CBO=\angle ACO=\alpha.$$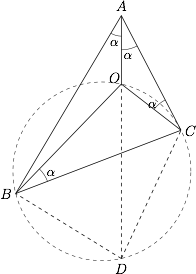
因为$$\angle ODC =\angle OBC=\angle CAO,$$所以 $\triangle CAD$ 是等腰三角形，$$AC=DC.$$又$$\angle CBD =\angle COD=\angle OAC+\angle OCA=2\alpha=\angle BAC, $$$$\angle BCD =\angle BOD=\angle OAB+\angle ABO=\angle ABC,$$所以$$\triangle ABC \backsim \triangle BCD,$$故$$\dfrac {AB}{BC}=\dfrac {BC}{CD}=\dfrac {CB}{AC},$$即$$BC^2=AB \cdot AC.$$
如图所示，延长 $AO$ 与 $\triangle BOC$ 的外接圆相交于点 $D$，连结 $BD$，$CD$，设$$\angle BAO =\angle CAO=\angle CBO=\angle ACO=\alpha.$$
因为$$\angle ODC =\angle OBC=\angle CAO,$$所以 $\triangle CAD$ 是等腰三角形，$$AC=DC.$$又$$\angle CBD =\angle COD=\angle OAC+\angle OCA=2\alpha=\angle BAC, $$$$\angle BCD =\angle BOD=\angle OAB+\angle ABO=\angle ABC,$$所以$$\triangle ABC \backsim \triangle BCD,$$故$$\dfrac {AB}{BC}=\dfrac {BC}{CD}=\dfrac {CB}{AC},$$即$$BC^2=AB \cdot AC.$$
答案
解析
备注
