$\triangle ABC$ 内接于 $\odot O$，$I$ 是三角形的内心，直线 $AI,BI$ 分别交 $\odot O$ 于 $D,E$，过点 $I$ 作直线 $l_1\parallel AB$，又过点 $C$ 作 $\odot O$ 的切线 $l_C$，若 $l_C$ 与 $l_I$ 相交于 $F$．证明：$D,E,F$ 三点共线．
【难度】
【出处】
2012年全国高中数学联赛山西省预赛
【标注】
【答案】
略
【解析】
设 $l_1$ 交 $DE$ 于 $F_1$，连接 $F_1C$，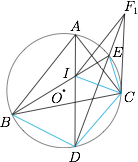
根据“鸡爪定理”，$$DC=DI,EC=EI,$$故 $\triangle IDE$ 与 $\triangle CDE$ 关于直线 $DE$ 对称，即直线 $DE$ 是线段 $IC$ 的中垂线，所以$$F_1I=F_1C,$$此时$$\angle DCP=180^\circ-\angle DCF_1=180^\circ-\angle DIF_1=\angle AIF_1=\angle IAB=\angle BCD=\angle CBD,$$因此据弦切角性质可知，直线 $CF_1$ 是 $\odot O$ 的切线，从而 $F,F_1$ 共点，即 $D,E,F$ 三点共线
根据“鸡爪定理”，$$DC=DI,EC=EI,$$故 $\triangle IDE$ 与 $\triangle CDE$ 关于直线 $DE$ 对称，即直线 $DE$ 是线段 $IC$ 的中垂线，所以$$F_1I=F_1C,$$此时$$\angle DCP=180^\circ-\angle DCF_1=180^\circ-\angle DIF_1=\angle AIF_1=\angle IAB=\angle BCD=\angle CBD,$$因此据弦切角性质可知，直线 $CF_1$ 是 $\odot O$ 的切线，从而 $F,F_1$ 共点，即 $D,E,F$ 三点共线
答案
解析
备注
