设椭圆 $\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1$（$a> b>0$）的中心为 $O$，其上两点 $P_1(x_1,y_1)$，$P_2(x_2,y_2)$ 满足 $\overrightarrow {OP_1}\perp \overrightarrow {OP_2}$．证明：$$\dfrac {1}{\left|\overrightarrow {OP_1}\right|^2}+\dfrac {1}{\left|\overrightarrow {OP_2}\right|^2}=\dfrac {1}{a^2}+\dfrac {1}{b^2}.$$
【难度】
【出处】
2014年全国高中数学联赛新疆维吾尔族自治区预赛
【标注】
【答案】
略
【解析】
设 $ \left|\overrightarrow {OP_i}\right|=r_i$，$ \overrightarrow {OP_i} $ 与 $x$ 轴的夹角为 $\theta_i$（如图所示），其中 $i=1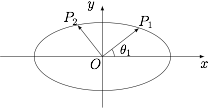,2$．
由 $\overrightarrow {OP_1}\perp \overrightarrow {OP_2} $ 可知，$$\theta_2=\dfrac {\pi}{2}+\theta_1.$$在平面直角坐标系 $xOy$ 中，有$$\begin{cases}x_1=r_1\cos \theta_1,\\ y_1=r_1\sin \theta_1,\end{cases} \begin{cases}x_2=r_2\cos \left(\dfrac {\pi}{2}+\theta_1\right) ,\\ y_2=r_2\sin \left(\dfrac {\pi}{2}+\theta_1\right).\end{cases}$$由于 $P_1$ 和 $P_2$ 在椭圆上，所以$$\begin{cases}\dfrac {x_1^2}{a^2}+\dfrac {y_1^2}{b^2}=r_1^2\left(\dfrac {\cos^2 \theta_1}{a^2}+\dfrac {\sin^2 \theta_1}{b^2}\right)=1,\\ \dfrac {x_2^2}{a^2}+\dfrac {y_2^2}{b^2}=r_2^2\left(\dfrac {\sin^2 \theta_1}{a^2}+\dfrac {\cos^2 \theta_1}{b^2}\right)=1, \end{cases}$$则$$\begin{cases} \dfrac {\cos^2 \theta_1}{a^2}+\dfrac {\sin^2 \theta_1}{b^2} =\dfrac {1}{r_1^2},\\ \dfrac {\sin^2 \theta_1}{a^2}+\dfrac {\cos^2 \theta_1}{b^2} =\dfrac {1}{r_2^2}, \end{cases}$$故有$$\dfrac {1}{r_1^2}+\dfrac {1}{r_2^2}=\dfrac {1}{a^2}+\dfrac {1}{b^2}.$$
由 $\overrightarrow {OP_1}\perp \overrightarrow {OP_2} $ 可知，$$\theta_2=\dfrac {\pi}{2}+\theta_1.$$在平面直角坐标系 $xOy$ 中，有$$\begin{cases}x_1=r_1\cos \theta_1,\\ y_1=r_1\sin \theta_1,\end{cases} \begin{cases}x_2=r_2\cos \left(\dfrac {\pi}{2}+\theta_1\right) ,\\ y_2=r_2\sin \left(\dfrac {\pi}{2}+\theta_1\right).\end{cases}$$由于 $P_1$ 和 $P_2$ 在椭圆上，所以$$\begin{cases}\dfrac {x_1^2}{a^2}+\dfrac {y_1^2}{b^2}=r_1^2\left(\dfrac {\cos^2 \theta_1}{a^2}+\dfrac {\sin^2 \theta_1}{b^2}\right)=1,\\ \dfrac {x_2^2}{a^2}+\dfrac {y_2^2}{b^2}=r_2^2\left(\dfrac {\sin^2 \theta_1}{a^2}+\dfrac {\cos^2 \theta_1}{b^2}\right)=1, \end{cases}$$则$$\begin{cases} \dfrac {\cos^2 \theta_1}{a^2}+\dfrac {\sin^2 \theta_1}{b^2} =\dfrac {1}{r_1^2},\\ \dfrac {\sin^2 \theta_1}{a^2}+\dfrac {\cos^2 \theta_1}{b^2} =\dfrac {1}{r_2^2}, \end{cases}$$故有$$\dfrac {1}{r_1^2}+\dfrac {1}{r_2^2}=\dfrac {1}{a^2}+\dfrac {1}{b^2}.$$
答案
解析
备注
