平面直角坐标 $xOy$ 中,$P$ 是不在 $x$ 轴上的一个动点,满足条件:过 $P$ 可作抛物线 $y^2=4x$ 的两条切线,两切点连线 $l_P$ 与 $PO$ 垂直.设直线 $l_P$ 与直线 $PO$,$x$ 轴的交点分别为 $Q$,$R$.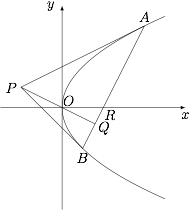

【难度】
【出处】
无
【标注】
-
证明:$R$ 是一个定点;标注答案略解析设 $P(a,b)(b\neq 0)$,易知 $a \neq 0$.
记两切点 $A(x_1,y_1)$,$B(x_2,y_2)$,则 $PA$,$PB$ 的方程分别为$$\begin{split}yy_1=2(x+x_1), \quad\cdots \cdots \text{ ① }\\yy_2=2(x+x_2), \quad\cdots \cdots \text{ ② }\end{split}$$而点 $P$ 的坐标 $(a,b)$ 同时满足 ①②,故 $A(x_1,y_1)$,$B(x_2,y_2)$ 均满足方程$$by =2(x+a), \quad\cdots \cdots \text{ ③ }$$故 ③ 就是直线 $AB$ 的方程.
直线 $PO$ 与 $AB$ 的斜率分别为 $\dfrac ba$ 与 $\dfrac 2b$,由 $PO \perp AB$ 知,$$\dfrac ba \cdot \dfrac 2b=-1,$$故 $a=-2$,从而 ③ 即为$$y=\dfrac 2b(x-2),$$因此 $AB$ 与 $x$ 轴的交点 $R$ 是定点 $(2,0)$. -
求 $\dfrac {|PQ|}{|QR|}$ 的最小值.标注答案$2\sqrt 2$解析因为 $a=-2$,所以直线 $PO$ 的斜率 $k_{1}=-\dfrac b2$,直线 $PR$ 的斜率 $k_{2}=-\dfrac b4$.
设 $\angle OPR=\alpha$,则 $\alpha$ 为锐角,且\[\begin{split}\dfrac {|PQ|}{|QR|}&=\dfrac {1}{\tan \alpha}=\left|\dfrac {1+k_1k_2}{k_1-k_2}\right|\\&=\dfrac {8+b^2}{2|b|}\geqslant \dfrac {2\sqrt {8\cdot b^2}}{2|b|}\\&=2\sqrt 2,\end{split}\]当 $b=\pm 2\sqrt 2$ 时,$\dfrac {|PQ|}{|QR|}$ 的最小值为 $2\sqrt 2$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2