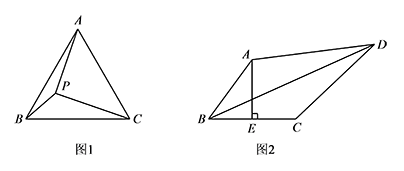
【难度】
【出处】
无
【标注】
-
如图1，在等边 $\triangle ABC$ 中，$AC=7$，点 $P$ 在 $\triangle ABC$ 内，且 $\angle APC=90^\circ$，$\angle BPC=120^\circ$，求 $\triangle APC$ 的面积．标注答案$\triangle APC$ 的面积为 $7\sqrt 3$解析如图，将 $\triangle ABP$ 绕点 $B$ 顺时针旋转 $60^\circ$ 至 $\triangle CBQ$，连接 $PQ$．
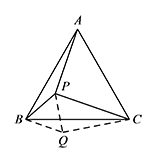显然 $\triangle PBQ$ 为等边三角形，
所以 $\angle BPQ=\angle BQP=60^\circ$．
而 $\angle BPC=120^\circ$，$\angle BQC=\angle BPA=150^\circ$，
所以 $\angle PQC=90^\circ$，$\angle QPC=60^\circ$．
令 $AP=CQ=\sqrt 3m$，则 $CP=2m$．
所以在 $\mathrm{Rt}\triangle APC$ 中，有 $(\sqrt 3m)^2+(2m)^2=7^2$，
解得 $m=\sqrt 7$，即 $AP=\sqrt{21}$，$CP=2\sqrt 7$．
从而 $S_{\triangle APC}=\dfrac 12AP\cdot CP=7\sqrt 3$． -
如图2，在四边形 $ABCD$ 中，$AE\perp BC$，垂足为点 $E$，$\angle BAE=\angle ADC$，$BE=CE=2$，$CD=5$，$AD=kAB$（$k$ 为常数），求 $BD$ 的长（用含 $k$ 的式子表示）．标注答案$BD$ 的长为 $\sqrt{16k^2+25}$解析如图，连接 $AC$，显然 $AC=AB$．
将 $\triangle ABD$ 绕点 $A$ 逆时针旋转 $\angle BAC$ 的度数至 $\triangle ACQ$，连接 $DQ$．
则 $\angle QAD=\angle BAC$，
所以 $\triangle ABC\backsim \triangle ADQ$，
从而 $DQ=kBC=4k$．
作 $AF\perp DQ$ 于点 $F$，则 $\angle DAF=\angle BAE=\angle ADC$，
所以 $AF\parallel CD$，
所以 $\angle CDQ=90^\circ$．
在 $\mathrm{Rt}\triangle CDQ$ 中，有 $CQ^2=(4k)^2+5^2$，
即 $BD=CQ=\sqrt{16k^2+25}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
