在 $\triangle ABC$ 中，$\angle BAC=60^\circ$．
【难度】
【出处】
无
【标注】
-
如图1，若 $AB=AC$，点 $P$ 在 $\triangle ABC$ 内，且 $PA=3$，$PC=4$，$\angle APC=150^\circ$，求 $PB$ 的长；标注答案$PB$ 的长为 $5$解析如图，将 $\triangle APC$ 绕点 $A$ 顺时针旋转 $60^\circ$ 得到 $\triangle AQB$，连接 $PQ$．
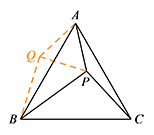易证 $\triangle PAQ$ 是等边三角形．
从而在 $\triangle PQB$ 中，有 $\angle PQB=90^\circ$，$PQ=3$，$BQ=4$，
所以 $PB=5$． -
如图2，若 $AB=AC$，点 $P$ 在 $\triangle ABC$ 外，且 $PA=3$，$PB=5$，$PC=4$，求 $\angle APC$ 的度数；标注答案$\angle APC$ 的度数为 $30^\circ$解析如图，将 $\triangle APC$ 绕点 $A$ 顺时针旋转 $60^\circ$ 得到 $\triangle AQB$，连接 $PQ$．
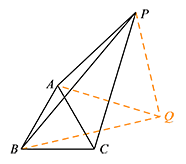易证 $\triangle PAQ$ 是等边三角形．
从而在 $\triangle PQB$ 中，有 $PQ=3$，$BQ=4$，$PB=5$．
所以 $\angle PQB=90^\circ$，
从而 $\angle APC=\angle AQB=30^\circ$． -
如图3，若 $AB=2AC$，点 $P$ 在 $\triangle ABC$ 内，且 $PA=\sqrt 3$，$PB=5$，$\angle APC=120^\circ$，求 $PC$ 的长．标注答案$PC$ 的长为 $2$解析如图，作 $\triangle AQC$，使得 $AQ=\dfrac 12 AP,CQ=\dfrac 12 BP$，连接 $PQ$．
易证 $\triangle ACB\sim \triangle AQP$．
从而在 $\triangle QPC$ 中，有 $\angle QPC=90^\circ$，$PQ=\dfrac 32$，$QC=\dfrac 52$，
所以 $PC=2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
