如图,已知 $B$,$C$,$E$ 三点在同一条直线上,$\triangle ABC$ 与 $\triangle DCE$ 都是等边三角形.其中线段 $BD$ 交 $AC$ 于点 $G$,线段 $AE$ 交 $CD$ 于点 $F$.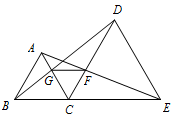

【难度】
【出处】
无
【标注】
-
求证:$\triangle ACE\cong \triangle BCD$;标注答案略解析因为 $\triangle ABC$ 与 $\triangle DCE$ 都是等边三角形,
所以 $AC=BC$,$CE =CD$,$\angle ACB =\angle DCE=60^\circ $,
所以 $\angle ACB+\angle ACD =\angle DCE+\angle ACD$,
即 $\angle ACE =\angle BCD$,
所以 $\triangle ACE\cong \triangle BCD$(${\mathrm {SAS}}$). -
求证:$\dfrac{AG}{GC}=\dfrac{AF}{FE}$.标注答案略解析因为 $\triangle ABC$ 与 $\triangle DCE$ 都是等边三角形,
所以 $AB=AC$,$CD=ED$,$\angle ABC =\angle DCE=60^\circ $,
所以 $\dfrac{AB}{CD}=\dfrac{AC}{ED}$,$AB\parallel DC$,
所以 $\angle ABG =\angle GDC$,$\angle BAG=\angle GCD$,
所以 $\triangle ABG\backsim \triangle CDG$,
所以 $\dfrac{AG}{GC}=\dfrac{AB}{CD}$.
同理,$\dfrac{AF}{FE}=\dfrac{AC}{DE}$.
所以 $\dfrac{AG}{GC}=\dfrac{AF}{FE}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2